
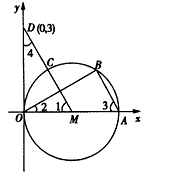
已知:如图,直径为OA的⊙M与x轴交于点O、A,点B、C把弧 CA分为三等份,连接MC并延长交y轴于点D(0,3)
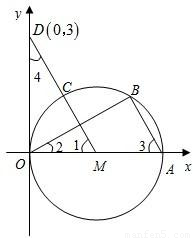
(1)求证:△OMD≌△BAO;
(2)若直线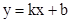 把⊙M的周长和△OMD面积均分为相等的两部份,求该直线的解析式.
把⊙M的周长和△OMD面积均分为相等的两部份,求该直线的解析式.
(1)证明见解析;(2)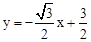 .
.
【解析】
试题分析:(1)连接BM,根据三等份,求出∠1、∠5、∠3、∠2的度数,推出∠1=∠3,根据直径求出∠OBA=∠DOM=90°,根据AAS求出全等即可;
(2)根据面积二等份,推出直线过M和(0,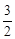 )点,求出OM,得出M的坐标,代入解析式求出即可.
)点,求出OM,得出M的坐标,代入解析式求出即可.
试题解析:(1)连接BM,
∵B、C把弧OA三等分,∴∠1=∠5=60°.
∵OM=BM,∴∠2=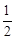 ∠5=30°.
∠5=30°.
∵OA为圆M的直径,∴∠ABO=90°. ∴AB=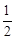 OA=OM,∠3=60°. ∴∠1=∠3,∠DOM=∠ABO=90°.
OA=OM,∠3=60°. ∴∠1=∠3,∠DOM=∠ABO=90°.
在△OMD和△BAO中,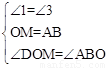 ,
,
∴△OMD≌△BAO.
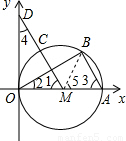
(2)若直线把圆M的面积分为二等份,则直线必过圆心M.
∵D(0,3),∠1=60°,OD=3, tan60°=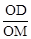 ,∴
,∴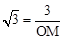 ,即
,即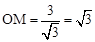 .
.
∴M(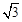 ,0).
,0).
把M(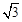 ,0)代入y=kx+b,得
,0)代入y=kx+b,得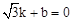 ,
,
又直线平分面积,必过点(0,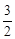 )代入得:
)代入得: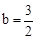 ,
,
二者联立解得: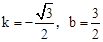 .
.
∴直线为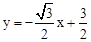 .
.
考点:1.圆周角定理;2.解二元一次方程组;3.直线上点的坐标与方程的关系;4.三角形的面积;5.全等三角形的判定和性质;6.圆心角、弧、弦的关系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 |
| OA |
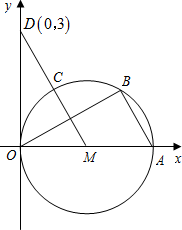 长交y轴于点D(0,3)
长交y轴于点D(0,3)| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
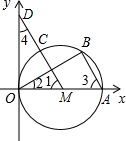 已知:如图,直径为OA的⊙M与x轴交于点O、A,点B、C把弧 CA分为三等份,连接MC并延长交y轴于点D(0,3)
已知:如图,直径为OA的⊙M与x轴交于点O、A,点B、C把弧 CA分为三等份,连接MC并延长交y轴于点D(0,3)查看答案和解析>>
科目:初中数学 来源:广东省中考真题 题型:解答题
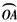 分为三等份,连接MC并延长交y轴于点D(0,3)。
分为三等份,连接MC并延长交y轴于点D(0,3)。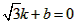 。
。 
查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省杭州市富阳市九年级(上)期中数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com