
 |
| OA |
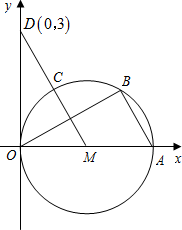 长交y轴于点D(0,3)
长交y轴于点D(0,3)| 3 |
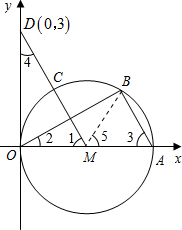 证明:(1)连接BM,∵B、C把
证明:(1)连接BM,∵B、C把 |
| OA |
| 1 |
| 2 |
| 1 |
| 2 |
|
| OD |
| tan60° |
| 3 | ||
|
| 3 |
| 3 |
| 3 |
| 3 |


科目:初中数学 来源: 题型:
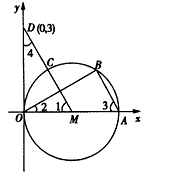
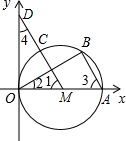 已知:如图,直径为OA的⊙M与x轴交于点O、A,点B、C把弧 CA分为三等份,连接MC并延长交y轴于点D(0,3)
已知:如图,直径为OA的⊙M与x轴交于点O、A,点B、C把弧 CA分为三等份,连接MC并延长交y轴于点D(0,3)查看答案和解析>>
科目:初中数学 来源:广东省中考真题 题型:解答题
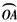 分为三等份,连接MC并延长交y轴于点D(0,3)。
分为三等份,连接MC并延长交y轴于点D(0,3)。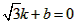 。
。 
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省余姚市六校九年级第一学期联考数学试卷(解析版) 题型:解答题
已知:如图,直径为OA的⊙M与x轴交于点O、A,点B、C把弧 CA分为三等份,连接MC并延长交y轴于点D(0,3)
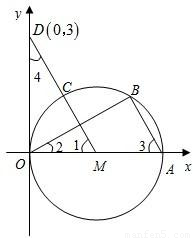
(1)求证:△OMD≌△BAO;
(2)若直线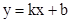 把⊙M的周长和△OMD面积均分为相等的两部份,求该直线的解析式.
把⊙M的周长和△OMD面积均分为相等的两部份,求该直线的解析式.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省杭州市富阳市九年级(上)期中数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com