
【题目】如图,已知⊙O的半径为2,弦BC的长为![]() ,点A为弦BC所对优弧上任意一点(B,C两点除外).
,点A为弦BC所对优弧上任意一点(B,C两点除外).
 (1)求∠BAC的度数;
(1)求∠BAC的度数;
(2)求△ABC面积的最大值.
(参考数据:![]() ,
,![]() ,
,![]() .)
.)
【答案】解:(1) 解法一
连接OB,OC,过O作OE⊥BC于点E.
∵OE⊥BC,BC=![]() ,
,
∴![]() . ………………1分
. ………………1分
 在Rt△OBE中,OB=2,∵
在Rt△OBE中,OB=2,∵![]() ,
,
∴![]() , ∴
, ∴![]() ,
,
∴![]() . ………………4分
. ………………4分
解法二
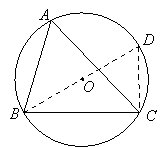
连接BO并延长,交⊙O于点D,连接CD.
∵BD是直径,∴BD=4,![]() .
.
在Rt△DBC中,![]() ,
,
∴![]() ,∴
,∴![]() .………………4分
.………………4分
(2) 解法一
因为△ABC的边BC的长不变,所以当BC边上的高最大时,△ABC的面积最大,此时点A落在优弧BC的中点处. ………………5分
过O作OE⊥BC于E,延长EO交⊙O于点A,则A为优弧BC的中点.连接AB,AC,则AB=AC,![]() .
.
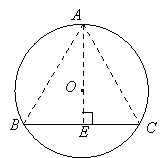 在Rt△ABE中,∵
在Rt△ABE中,∵![]() ,
,
∴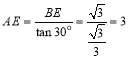 ,
,
∴S△ABC=![]() .
.
答:△ABC面积的最大值是![]() . ………………7分
. ………………7分
解法二
因为△ABC的边BC的长不变,所以当BC边上的高最大时,△ABC的面积大,此时点A落在优弧BC的中点处. ………………5分
过O作OE⊥BC于E,延长EO交⊙O于点A,则A为优弧BC的中点.连接AB,AC,则AB=AC.
∵![]() , ∴△ABC是等边三角形.
, ∴△ABC是等边三角形.
在Rt△ABE中,∵![]() ,
,
∴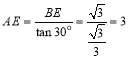 ,
,
∴S△ABC=![]() .
.
答:△ABC面积的最大值是![]() . ………………7分
. ………………7分
【解析】略


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】小明去离家2.4 km的体育馆看球赛,进场时,发现门票还放在家中,此时离比赛还有45 min,于是他立即步行(匀速)回家取票,在家取票用时2 min,取到票后,他马上骑自行车(匀速)赶往体育馆.已知小明骑自行车从家赶往体育馆比从体育馆步行回家所用时间少20 min,骑自行车的速度是步行速度的3倍.
(1)小明步行的速度是多少?
(2)小明能否在球赛开始前赶到体育馆?
查看答案和解析>>
科目:初中数学 来源: 题型:
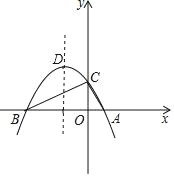
【题目】如图,抛物线y=﹣![]() x2+bx+2与x轴交于A,B两点,与y轴交于C点,且点A的坐标为(1,0).
x2+bx+2与x轴交于A,B两点,与y轴交于C点,且点A的坐标为(1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,并证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM的周长最小时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市2017年国内生产总值(GDP)比2016年增长了12%,由于受到国际金融危机的影响,预计2018比2017年增长7%,若这两年GDP年平均增长率为![]() %,则
%,则![]() %满足的关系是( )
%满足的关系是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区商店以2元的批发价进了一批纪念品.经调查发现,每个定价3元,每天可以能卖出500件,而且定价每上涨0.1元,其销售量将减少10件.根据规定:纪念品售价不能超过批发价的2.5倍.
(1)当每个纪念品定价为3.5元时,商店每天能卖出________件;
(2)如果商店要实现每天800元的销售利润,那该如何定价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k+1)x+4(k﹣![]() )=0.
)=0.
(1)判断这个一元二次方程的根的情况;
(2)若等腰三角形的一边长为3,另两条边的长恰好是这个方程的两个根,求这个等腰三角形的周长及面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b分别交x轴正半轴、y轴正半轴于点A、B,点P在边OA上运动(点P不与点O,A重合),PE⊥AB于点E,点F,P关于直线OE对称,PE:EA=3:4.若EF∥OA,且四边形OPEF的周长为6.

(1)求证:四边形OPEF为菱形;
(2)求证:OB=BE;
(3)求一次函数y=kx+b的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com