练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．化简：$\frac{\sqrt{2}+\sqrt{3}}{\sqrt{10}+\sqrt{14}+\sqrt{15}+\sqrt{21}}$．

    分析 我们可以先将分母因式分解，约分后再化简．

    解答 解：$\frac{\sqrt{2}+\sqrt{3}}{\sqrt{10}+\sqrt{14}+\sqrt{15}+\sqrt{21}}$
    =$\frac{\sqrt{2}+\sqrt{3}}{\sqrt{2}（\sqrt{5}+\sqrt{7}）+\sqrt{3}（\sqrt{5}+\sqrt{7}）}$，
    =$\frac{\sqrt{2}+\sqrt{3}}{（\sqrt{2}+\sqrt{3}）（\sqrt{5}+\sqrt{7}）}$，
    =$\frac{1}{\sqrt{5}+\sqrt{7}}$，
    =$\frac{\sqrt{7}-\sqrt{5}}{2}$．

    点评 此题主要考查分母有理化，把分母分组分解是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    18．如图，一定数量的石子可以摆成如图所示的三角形和四边形，古希腊科学家把数1，3，6，10，15，21，…，称为“三角形数”；把1、4、9、16，25，…称为“正方形数”．同样的，可以把数1，5，12，22，…，等数称为“五边形数”．

    将三角形、正方形、五边形都整齐的由左到右填在所示表格里：
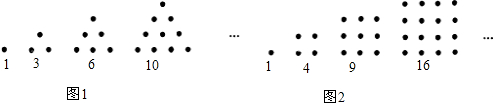
    三角形数136101521a…
    正方形数1491625b49…
    五边形数151222C5170…
    （1）按照规律，表格中a=28，b=36，c=35．
    （2）观察表中规律，第n个“正方形数”是n2；若第n个“三角形数”是x，则用含x、n的代数式表示第n个“五边形数”是n2+x-n．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．若x2-2kx+25是一个完全平方式，则k=（　　）
    A．10B．±10C．5D．±5

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

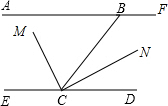    16．如图：AF∥DE，B为AF上的一点，∠ABC=60°交ED于C，CM平分∠BCE，∠MCN=90°，
    （1）∠DCN的度数；
    （2）若∠CBF的平分线交CN于N，求证：BN∥CM．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知抛物线y=x2+（a-3）x+（3b-a）与x轴有唯一的公共点A（3，0），求实数a、b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．以菱形ABCD的一个顶点A为圆心，以边AB长为半径画圆，被菱形截得的$\widehat{BD}$是40°，则菱形的一个钝角是（　　）
    A．140°B．160°C．100°D．150°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．已知a=2-$\sqrt{3}$，b=2+$\sqrt{3}$，计算$\frac{a+\sqrt{ab}}{b+\sqrt{ab}}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．已知抛物线y=x2-2x-3．
    （1）求抛物线与x轴的交点坐标；
    （2）利用图象说明，当x为何值时，y＞0？y=0？y＜0？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

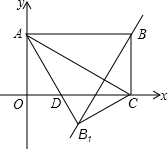    19．如图，矩形OABC在平面直角坐标系中，并且OA、OC的长满足：|OA-2$\sqrt{3}$|+（OC-6）2=0．
    （1）求A、B、C三点的坐标．
    （2）把△ABC沿AC对折，点B落在点B1处，AB1与x轴交于点D，求直线BB1的解析式．
    （3）在直线AC上是否存在点P使PB1+PD的值最小？若存在，请找出点P的位置，并求出PB1+PD的最小值；若不存在，请说明理由．
    （4）在直线AC上是否存在点P使|PD-PB|的值最大？若存在，请找出点P的位置，并求出|PD-PB|最大值．

    查看答案和解析>>

    同步练习册答案