
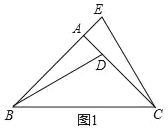
【题目】如图1,在△ABC中,∠BAC=90°,点D在AC上,点E在BA的延长线上,连接BD,CE,AD=AE,BD=CE.
(1)若BD=![]() ,AD=1,求BC的长度;
,AD=1,求BC的长度;
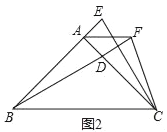
(2)将图1中的BD延长,过点A作AF∥BC交BD延长线于点F,如图2,连接FC,若BC=BF,求证:CD=CF.
【答案】(1)4![]() ;(2)见解析
;(2)见解析
【解析】试题分析:(1)根据直角三角形全等的判定HL证得Rt△BAD≌Rt△CAE,根据全等三角形的性质得出AB=AC,然后根据勾股定理得到AB的长,进而求出BC的长;
(2)作AM⊥BC于M,FN⊥BC于N.易知四边形AMNF是矩形,再根据矩形的性质和等腰三角形的三线合一的性质求解即可.
试题解析:(1)解:在Rt△BAD和△RtCAE中,
![]() ,
,
∴Rt△BAD≌Rt△CAE,
∴AB=AC,
∵AB=![]() =
=![]() =4,
=4,
∴BC=![]() AB=4
AB=4![]() .
.
(2)作AM⊥BC于M,FN⊥BC于N.
∵AF∥BC,易知四边形AMNF是矩形,
∴AM=FN,
∵AB=AC,AM⊥BC,
∴AM=FN=![]() BC=
BC=![]() BF,
BF,
∴∠FBN=30°,
∵BF=BC,
∴∠BFC=∠BCFF=75°,
∵∠CDF=∠DBC+∠DCB=30°+45°=75°,
∴∠CDF=∠CFD,
∴CD=CF.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1在正方形ABCD的外侧作两个等边三角形ADE和DCF,连接AF,BE.
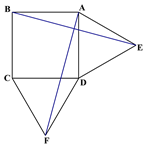
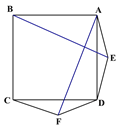

(图1) (图2) (备用图)
(1)请判断:AF与BE的数量关系是_____________,位置关系______________;
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予证明;
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
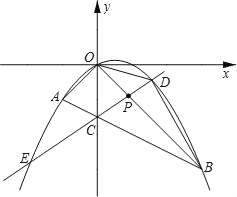
【题目】如图,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2﹣2x﹣3=0的两根.
(1)求抛物线的解析式;
(2)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.
①当△OPC为等腰三角形时,求点P的坐标;
②求△BOD 面积的最大值,并写出此时点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开阔学生的视野,积极组织学生参加课外读书活动.“放飞梦想”读书小组协助老师随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他等四类),并将调查结果绘制成如下两幅不完整的统计图,请你结合图中的信息解答下列问题:
(1)求被调查的学生人数;
(2)补全条形统计图;
(3)已知该校有1200名学生,估计全校最喜爱文学类图书的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
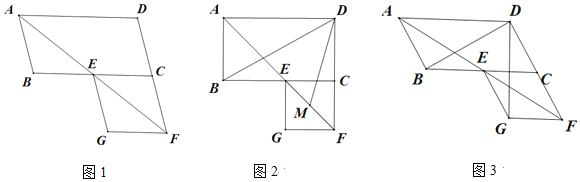
【题目】在平行四边形ABCD中,∠BAD的平分线交线段BC于点E,交线段DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.
(1)如图1,证明平行四边形ECFG为菱形;
(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;
(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强与小刚都住在安康小区,在同一所学校读书.某天早上,小强![]() 从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留
从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留![]() 分钟,校车行驶途中始终保持匀速.当天早上,小刚
分钟,校车行驶途中始终保持匀速.当天早上,小刚![]() 从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早
从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早![]() 分钟到学校站点.他们乘坐的车辆从安康小区站出发所行驶路程
分钟到学校站点.他们乘坐的车辆从安康小区站出发所行驶路程![]() (千米)与行驶时间
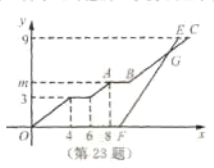
(千米)与行驶时间![]() (分钟)之间的函数图象如图所示.
(分钟)之间的函数图象如图所示.
(1)求点![]() 的纵坐标
的纵坐标![]() 的值;
的值;
(2)小刚乘坐出租车出发后经过多少分钟追到小强所乘坐的校车?并求此时他们距学校站点的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
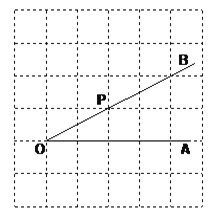
【题目】如图,点P是![]() 的边OB上的一点。
的边OB上的一点。
过点P画OA的垂线,垂足为H;
过点P画OB的垂线,交OA于点C;
线段PH的长度是点P到 的距离,_____ 是点C到直线OB的距离。因为直线外一点到直线上各点连接的所有线段中,垂线段最短,所以线段PC、PH、OC这三条线段大小关系是 。(用“<”号连接)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学复习课上,老师出示5张背面完全相同的卡片,卡片正面分别写有下列方程:
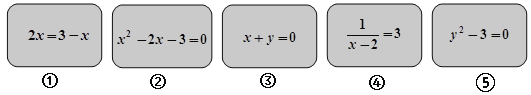
(1)若把这5张卡片的背面朝上且搅匀,从中随机抽取一张卡片,则抽到卡片上有一元二次方程的概率是多少?
(2)请按一定的规则把这5个方程分成两类,写出你的分类规则,并把分类结果分别填在下列两个大括号内(只需填方程的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com