
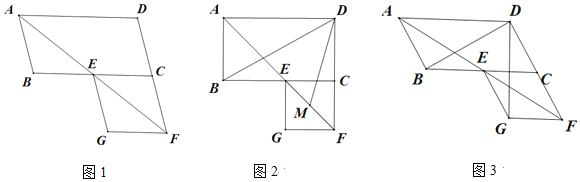
【题目】在平行四边形ABCD中,∠BAD的平分线交线段BC于点E,交线段DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.
(1)如图1,证明平行四边形ECFG为菱形;
(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;
(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.
【答案】(1)证明见解析;
(2)∠BDM的度数为45°;
(3)∠BDG的度数为60°.
【解析】试题分析:(1)平行四边形的性质可得AD∥BC,AB∥CD,再根据平行线的性质证明∠CEF=∠CFE,根据等角对等边可得CE=CF,再有条件四边形ECFG是平行四边形,可得四边形ECFG为菱形;
(2)首先证明四边形ECFG为正方形,再证明△BME≌△DMC可得DM=BM,∠DMC=∠BME,再根据∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°可得到∠BDM的度数;
(3)延长AB、FG交于H,连接HD,求证平行四边形AHFD为菱形,得出△ADH,△DHF为全等的等边三角形,证明△BHD≌△GFD,即可得出答案.
试题解析:(1)∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形.
(2)如图,连接BM,MC,
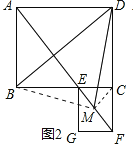
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵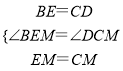
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形,
∴∠BDM=45°;
(3)∠BDG=60°,
延长AB、FG交于H,连接HD.

∵AD∥GF,AB∥DF,
∴四边形AHFD为平行四边形,
∵∠ABC=120°,AF平分∠BAD,
∴∠DAF=30°,∠ADC=120°,∠DFA=30°,
∴△DAF为等腰三角形,
∴AD=DF,
∴平行四边形AHFD为菱形,
∴△ADH,△DHF为全等的等边三角形,
∴DH=DF,∠BHD=∠GFD=60°,
∵FG=CE,CE=CF,CF=BH,
∴BH=GF,
在△BHD与△GFD中,
∵ ,
,
∴△BHD≌△GFD(SAS),
∴∠BDH=∠GDF
∴∠BDG=∠BDH+∠HDG=∠GDF+∠HDG=60°.


科目:初中数学 来源: 题型:
【题目】【背景】已知:l∥m∥n∥k,平行线l与m、m与n、n与k之间的距离分别为d1,d2,d3,且d1=d3=1,d2=2.我们把四个顶点分别在l,m,n,k这四条平行线上的四边形称为“格线四边形” .
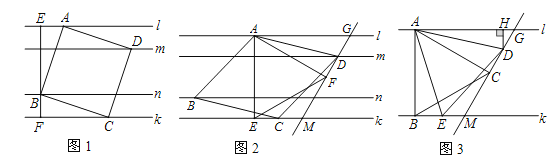
【探究1】(1)如图1,正方形ABCD为“格线四边形”,BE⊥l于点E,BE的反向延长线交直线k于点F.求正方形ABCD的边长.
【探究2】(2)如图2,菱形ABCD为“格线四边形”且∠ADC=60°,△AEF是等边三角形,AE⊥k于点E,∠AFD=90°,直线DF分别交直线l,k于点G、点M.求证:EC=DF.
【拓展】(3)如图3,l∥k,等边△ABC的顶点A,B分别落在直线l,k上,AB⊥k于点B,且∠ACD=90°,直线CD分别交直线l、k于点G、点M,点D、点E分别是线段GM、BM上的动点,且始终保持AD=AE,DH⊥l于点H.猜想:DH在什么范围内,BC∥DE?并说明此时BC∥DE的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
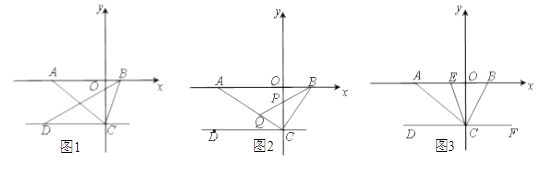
【题目】如图1,在平面直角坐标系中,点![]() 为
为![]() 轴负半轴上一点,点
轴负半轴上一点,点![]() 为
为![]() 轴正半轴上一点,
轴正半轴上一点,![]() ,
,![]() ,其中
,其中![]() ,
,![]() 满足关系式:
满足关系式:![]() +
+![]() .
.
(1)![]() = ,
= ,![]() = ,△
= ,△![]() 的面积为 ;
的面积为 ;
(2)如图2,若![]() ⊥
⊥![]() ,点
,点![]() 线段
线段![]() 上一点,连接
上一点,连接![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,当∠
,当∠![]() =∠
=∠![]() 时,求证:
时,求证:![]() 平分∠
平分∠![]() ;
;
(3)如图3,若![]() ⊥
⊥![]() ,点
,点![]() 是点
是点![]() 与点
与点![]() 之间一动点,连接
之间一动点,连接![]() ,
,![]() 始终平分∠
始终平分∠![]() ,当点
,当点![]() 在点
在点![]() 与点
与点![]() 之间运动时,
之间运动时,![]() 的值是否变化?若不变,求出其值;若变化,请说明理由.
的值是否变化?若不变,求出其值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
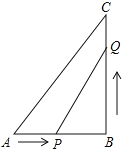
【题目】已知:如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,同时点Q从点B开始沿BC边向点C以2cm/s的速度移动.当一个点到达终点时另一点也随之停止运动,设运动时间为x秒,
(1)求几秒后,△PBQ的面积等于6cm2?
(2)求几秒后,PQ的长度等于5cm?
(3)运动过程中,△PQB的面积能否等于8cm2?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )

A. 0.324πm2 B. 0.288πm2 C. 1.08πm2 D. 0.72πm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于任意两点A(x1,y1)B (x2,y2),规定运算:
(1)A⊕B=(x1+x2,y1+y2);
(2)A⊙B=x1x2+y1y2;
(3)当x1=x2且y1=y2时,A=B.
有下列四个命题:
①若有A(1,2),B(2,﹣1),则A⊕B=(3,1),A⊙B=0;
②若有A⊕B=B⊕C,则A=C;
③若有A⊙B=B⊙C,则A=C;
④(A⊕B)⊕C=A⊕(B⊕C)对任意点A、B、C均成立.
其中正确的命题为______(只填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两名同学在调查时使用下面两种提问方式,你认为哪一种更好些( )
A. 难道你不认为科幻片比武打片更有意思吗?
B. 你更喜欢哪一类电影 ——科幻片还是武打片?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com