
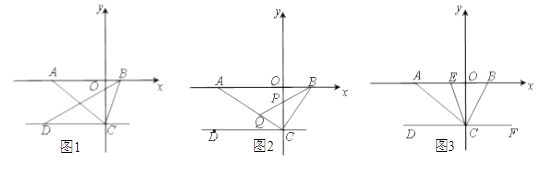
【题目】如图1,在平面直角坐标系中,点![]() 为
为![]() 轴负半轴上一点,点
轴负半轴上一点,点![]() 为
为![]() 轴正半轴上一点,
轴正半轴上一点,![]() ,
,![]() ,其中
,其中![]() ,
,![]() 满足关系式:
满足关系式:![]() +
+![]() .
.
(1)![]() = ,
= ,![]() = ,△
= ,△![]() 的面积为 ;
的面积为 ;
(2)如图2,若![]() ⊥
⊥![]() ,点
,点![]() 线段
线段![]() 上一点,连接
上一点,连接![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,当∠
,当∠![]() =∠
=∠![]() 时,求证:
时,求证:![]() 平分∠
平分∠![]() ;
;
(3)如图3,若![]() ⊥
⊥![]() ,点
,点![]() 是点
是点![]() 与点
与点![]() 之间一动点,连接
之间一动点,连接![]() ,
,![]() 始终平分∠
始终平分∠![]() ,当点
,当点![]() 在点
在点![]() 与点
与点![]() 之间运动时,
之间运动时,![]() 的值是否变化?若不变,求出其值;若变化,请说明理由.
的值是否变化?若不变,求出其值;若变化,请说明理由.
【答案】(1)![]() =-3,
=-3,![]() = -4,△
= -4,△![]() 的面积为6; (2)证明见解析;
的面积为6; (2)证明见解析;
(3) ![]() 的值是定值,
的值是定值,![]() =2,理由见解析.
=2,理由见解析.
【解析】试题分析:(1)由非负数的性质即可求出a、b的值,由题意可得DC的长以及DC边上的高,根据三角形的面积公式即可求得;
(2)由AC⊥BC可得∠CBQ+∠CQP=90°,又∠OBP+∠OPB=90°,∠OPB=∠CPQ,∠CPQ=∠CQP从而可得∠CBQ=∠OBP,从而问题得证;
(3)由AC⊥BC,可得∠ACB=90°,从而可得∠ACD+∠BCF=90°,由CB平分∠ECF可得∠ACD+∠ECB=90°,而已知∠ACE+∠ECB=90°,从而可得∠ACD=∠ACE,得∠DCE=2∠ACD,
从而能够得到∠ACD=∠BCO, 由已知可得CD//AB,从而得到结论.
试题解析:(1)![]() = -3,
= -3,![]() =-4,△
=-4,△![]() 的面积为6;
的面积为6;
(2)∵AC⊥BC,∴∠CBQ+∠CQP=90°,又∵∠OBP+∠OPB=90°,∠OPB=∠CPQ,
∴∠CPQ+∠OBP=90°,又∵∠CPQ=∠CQP,∴∠CBQ=∠OBP,∴BP平分∠ABC ;
(3) ![]() 的值是定值,
的值是定值,![]() =2,理由如下:
=2,理由如下:
∵AC⊥BC,∴∠ACB=90°,∴∠ACD+∠BCF=90°,
又∵CB平分∠ECF,∴∠ECB=∠BCF,∴∠ACD+∠ECB=90°,
又∵∠ACE+∠ECB=90°,∴∠ACD=∠ACE,∴∠DCE=2∠ACD,
又∵∠ACD+∠ACO=90°,∠BCO+∠ACO=90°,∴∠ACD=∠BCO,
又∵C(0,-3),D(-4,-3), ∴CD//AB,∴∠BEC=∠DCE=2∠ACD,∴∠BEC=2∠BCO,
∴![]() =2.
=2.


科目:初中数学 来源: 题型:
【题目】下列各式中,计算结果是x2+7x -18的是( )
A.(x-1)(x+18)
B.(x+2)(x+9)
C.(x-3)(x+6)
D.(x-2)(x+9)
查看答案和解析>>
科目:初中数学 来源: 题型:
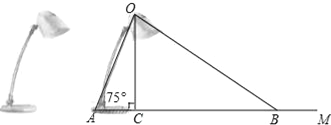
【题目】如图为放置在水平桌面上的台灯的平面示意图,灯臂AO长为40cm,与水平面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°,求该台灯照亮水平面的宽度BC(不考虑其他因素,结果精确到0.1cm.温馨提示:sin75°≈0.97,cos75°≈0.26,![]() ≈1.73).
≈1.73).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在电影票上,将7排6号“简记作(7,6)”
(1)6排7号可表示为___________;(2) (8,6)表示的意义是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第四届高淳国际慢城金花旅游节期间,全区共接待游客686000人次.将686000用科学记数法表示为( )
A. 686×104 B. 68.6×105 C. 6.86×105 D. 6.86×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=![]() 的图象与直线y=﹣x+b都经过点A(1,4),且该直线与x轴的交点为B.
的图象与直线y=﹣x+b都经过点A(1,4),且该直线与x轴的交点为B.
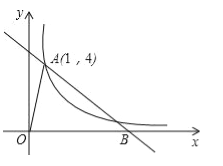
(1)求反比例函数和直线的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
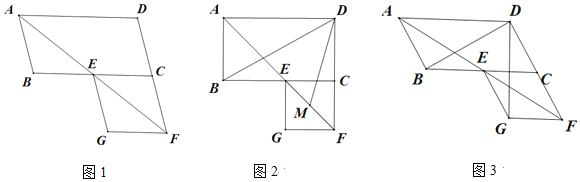
【题目】在平行四边形ABCD中,∠BAD的平分线交线段BC于点E,交线段DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.
(1)如图1,证明平行四边形ECFG为菱形;
(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;
(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.易证:CE=CF.
(1)在图1中,若G在AD上,且∠GCE=450.试猜想GE,BE,GD三线段之间的数量关系,并证明你的结论.
(2)运用(1)中解答所积累的经验和知识,完成下面两题:
①如图2,在四边形ABCD中∠B=∠D=900,BC=CD,点E,点G分别是AB边,AD边上的动点.若∠BCD=α,∠ECG=β,试探索当α和β满足什么关系时,图1中GE,BE,GD三线段之间的关系仍然成立,并说明理由.
②在平面直角坐标中,边长为1的正方形OABC的两顶点A,C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图3).设△MBN的周长为p,在旋转正方形OABC的过程中,p值是否有变化?若不变,请直接写出结论.
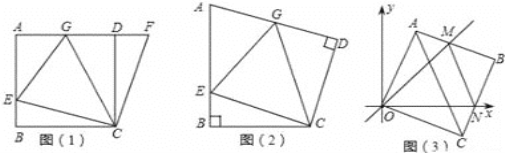
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com