
| A. | $\frac{a}{c}=\frac{d}{b}$ | B. | $\frac{c}{a}=\frac{ac}{bd}$ | C. | $\frac{a+2b}{b}=\frac{c+2d}{d}$ | D. | $\frac{a+1}{b}=\frac{c+1}{d}$ |
分析 由于$\frac{a}{b}=\frac{c}{d}$,由此得到ad=bc,将A、B、C、D中的比例式也可以化成等积式,然后化简即可判定是否正确.
解答 解:∵$\frac{a}{b}=\frac{c}{d}$,∴ad=bc,
A、$\frac{a}{c}$=$\frac{d}{b}$可变为ab=cd,故A错误;
B、$\frac{c}{a}$=$\frac{ac}{bd}$可以变为cbd=a2c,化简为bd=a2,故B错误;
C、$\frac{a+2b}{b}$=$\frac{c+2d}{d}$可以变为ad+2bd=bc+2bd,进一步得到ad=bc,故C正确;
D、$\frac{a+1}{b}$=$\frac{c+1}{d}$可以变为ad+d=bc+b,进一步得到b=d,故D错误.
故选C.
点评 此题主要考查了比例的基本性质,解答此类题一定要熟练掌握比例的基本性质才能比较好解决这类问题.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AD平分∠BAC,DG⊥BC且平分BC于点G,DE⊥AB于E,
如图,在△ABC中,AD平分∠BAC,DG⊥BC且平分BC于点G,DE⊥AB于E,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
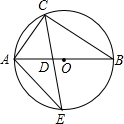 如图,△ABC内接于⊙O,AB是⊙O的直径,CE平分∠ACB交⊙O于点E,∠E=30°,交AB于点D,连接AE,则SADC:S△ADE的比值为( )
如图,△ABC内接于⊙O,AB是⊙O的直径,CE平分∠ACB交⊙O于点E,∠E=30°,交AB于点D,连接AE,则SADC:S△ADE的比值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com