解:(1)原式=

a
2bc
3•4a
4b
4c
2=2a
6b
5c
5;
(2)原式=3x-6y-2;
(3)原式=(2x)
2-(3y)
2-(2x+3y)
2,
=4x
2-9y
2-(4x
2+9y
2+12xy),
=4x
2-9y
2-4x
2-9y
2-12xy,
=-18y
2-12xy;
(4)原式=2005×2005-2006×(2005-1),
=2005×2005-2006×2005+2006,
=2005×(2005-2006)+2006,
=1.
分析:(1)根据同底数幂的乘法法则与幂的乘方法则进行计算;
(2)根据多项式除以单项式的法则进行计算;
(3)根据平方差公式与完全平方和公式进行计算;
(4)把2004看成(2005-1)进行计算.
点评:本题考查了积的乘方的性质,单项式的乘法,多项式除单项式,完全平方公式和平方差公式,计算时要严格根据整式的运算法则运算,同时要注意去括号法则和乘方的运算性质的运用.

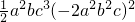
 a2bc3•4a4b4c2=2a6b5c5;
a2bc3•4a4b4c2=2a6b5c5;

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案