
分析 (1)根据配方法进行解答方程即可;
(2)根据公式法解答方程;
(3)移项根据因式分解法中的提公因式法解答方程即可;
(4)先去括号化简,再根据因式分解法解答方程即可.
解答 解:(1)2x2+5x-3=0
2x2+5x=3
$2(x+\frac{5}{2}x)=3$
$2(x+\frac{5}{4})^{2}=\frac{49}{8}$
$(x+\frac{5}{4})^{2}=\frac{49}{16}$
$x+\frac{5}{4}=±\frac{7}{4}$
$x=-\frac{5}{4}±\frac{7}{4}$
∴${x}_{1}=-3,{x}_{2}=\frac{1}{2}$;
(2)2x2-4x-1=0
a=2,b=-4,c=-1,
△=(-4)2-4×2×(-1)=24>0,
x=$\frac{-(-4)±\sqrt{24}}{2×2}=\frac{4±2\sqrt{6}}{4}=\frac{2±\sqrt{6}}{2}$,
∴${x}_{1}=\frac{2+\sqrt{6}}{2},{x}_{2}=\frac{2-\sqrt{6}}{2}$;
(3)x(5x+4)=5x+4
x(5x+4)-(5x+4)=0
(5x+4)(x-1)=0
∴5x+4=0或x-1=0,
∴${x}_{1}=-\frac{4}{5},{x}_{2}=1$;
(4)(2x+3)(x-2)=4
2x2-x-10=0
(2x-5)(x+2)=0
∴2x-5=0或x+2=0
∴${x}_{1}=\frac{5}{2},{x}_{2}=-2$.
点评 本题考查解一元二次方程,解题的关键是明确解一元二次方程的几种解答方法,配方法、公式法、因式分解法.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
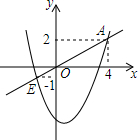 如图,二次函数y=x2+bx+c的图象与正比例函数y=kx的图象相交于点A(4,2)和点B(m,-1),求该二次函数与正比例函数的解析式.
如图,二次函数y=x2+bx+c的图象与正比例函数y=kx的图象相交于点A(4,2)和点B(m,-1),求该二次函数与正比例函数的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2(x+1)2 | B. | y=4x2-(2x+1)2 | C. | y=$\frac{{x}^{2}}{x}$ | D. | y=$\frac{1}{{x}^{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com