
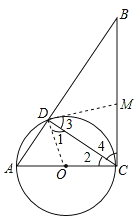
【题目】在RT△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,连接CD.

(1)求证:∠DCB=∠A;
(2)若M为线段BC上一点,试问点M在什么位置时,直线DM与⊙O相切?并说明理由。
【答案】(1)证明见解析;(2)当MC=MD(或点M是BC的中点)时,直线DM与⊙O相切.理由见解析.
【解析】
试题分析:(1)根据圆周角定理可得∠ADC=90°,再根据直角三角形的性质可得∠A+∠DCA=90°,再由∠DCB+∠ACD=90°,可得∠DCB=∠A;
(2)当MC=MD时,直线DM与⊙O相切,连接DO,根据等等边对等角可得∠1=∠2,∠4=∠3,再根据∠ACB=90°可得∠1+∠3=90°,进而证得直线DM与⊙O相切.
试题解析:(1)∵AC为直径,
∴∠ADC=90°,
∴∠A+∠DCA=90°,
∵∠ACB=90°,
∴∠DCB+∠ACD=90°,
∴∠DCB=∠A;
(2)当MC=MD(或点M是BC的中点)时,直线DM与⊙O相切;
连接DO,
∵DO=CO,
∴∠1=∠2,
∵DM=CM,
∴∠4=∠3,
∵∠2+∠4=90°,
∴∠1+∠3=90°,
∴直线DM与⊙O相切,
故当MC=MD(或点M是BC的中点)时,直线DM与⊙O相切.


科目:初中数学 来源: 题型:
【题目】某市为提倡节约用水,采取分段收费.若每户每月用水量不超过20 m3,每立方米收费2元;若用水量超过20 m3,超过部分每立方米加收1元.小明家5月份交水费64元,则他家该月用水________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线互相平分的四边形是平行四边形
D.对角线互相垂直平分的四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( )

A.6 B.7 C.8 D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-![]() +
+![]() +4的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
+4的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
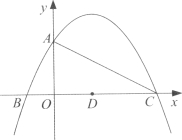
(1)点A的坐标为_______ ,点C的坐标为_______ ;
(2)线段AC上是否存在点E,使得△EDC为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由;
(3)点P为x轴上方的抛物线上的一个动点,连接PA、PC,若所得△PAC的面积为S,则S取何值时,相应的点P有且只有2个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=5,BC=12,点A在⊙B上,如果⊙D与⊙B相交,且点B在⊙D内,那么⊙D的半径长可以等于 .(只需写出一个符合要求的数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚和小强相约晨练跑步,小刚比小强早1分钟离开家门,3分钟后迎面遇到从家跑来的小强.两人同路并行跑了2分钟后,决定进行长跑比赛,比赛时小刚的速度始终是180米/分,小强的速度始终是220米/分.下图是两人之间的距离y(米)与小刚离开家的时间x(分钟)之间的函数图象,根据图象回答下列问题:

(1)两人相遇之前,小刚的速度是 米/分,小强的速度是 米/分;
(2)求两人比赛过程中y与x之间的函数关系式;
(3)若比赛开始10分钟后,小强按原路以比赛时的速度返回,则再经过多少分钟两人相遇?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com