
【题目】如图,AD是△ABC的边BC上的高,∠B=60°,∠C=45°,AC=6.求:
(1)AD的长;
(2)△ABC的面积.

【答案】(1)AD=3![]() ;(2)S△ABC=9+3
;(2)S△ABC=9+3![]() .
.
【解析】试题分析:(1)根据三角形内角和可得∠DAC=45°,根据等角对等边可得AD=CD,然后再根据勾股定理可计算出AD的长;
(2)根据三角形内角和可得∠BAD=30°,再根据直角三角形的性质可得AB=2BD,然后利用勾股定理计算出BD的长,进而可得BC的长,然后利用三角形的面积公式计算即可.
解:(1)∵∠C=45°,AD是△ABC的边BC上的高,∴∠DAC=45°,∴AD=CD.
∵AC2=AD2+CD2,∴62=2AD2,∴AD=3![]() .
.
(2)在Rt△ADB中,∵∠B=60°,∴∠BAD=30°,∴AB=2BD.
∵AB2=BD2+AD2,∴(2BD)2=BD2+AD2,BD=![]() .
.
∴S△ABC=![]() BC·AD=
BC·AD=![]() (BD+DC)·AD=
(BD+DC)·AD=![]() ×(
×(![]() +3
+3![]() )×3
)×3![]() =9+3
=9+3![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD,∠A=60°,AB=4,以点B为圆心的扇形与边CD相切于点E,扇形的圆心角为60°,点E是CD的中点,图中两块阴影部分的面积分别为S1 , S2 , 则S2﹣S1= . 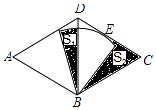
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现与探索。
(1)根据小明的解答将下列各式因式分解

① a2-12a+20;②(a-1)2-8(a-1)+7;③ a2-6ab+5b2
(2)根据小丽的思考解决下列问题:

①说明:代数式a2-12a+20的最小值为-16.
②请仿照小丽的思考解释代数式-(a+1)2+8的最大值为8,并求代数式-a2+12a-8的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,过等边三角形ABC边AB上一点D作DE∥BC交边AC于点E,分别取BC,DE的中点M,N,连接MN.
(1)发现:在图1中, ![]() =;
=;
(2)应用:如图2,将△ADE绕点A旋转,请求出 ![]() 的值;
的值;
(3)拓展:如图3,△ABC和△ADE是等腰三角形,且∠BAC=∠DAE,M,N分别是底边BC,DE的中点,若BD⊥CE,请直接写出 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,双曲线:y= ![]() (x>0)分别与直线OA:y=x和直线AB:y=﹣x+10,交于C,D两点,并且OC=3BD.
(x>0)分别与直线OA:y=x和直线AB:y=﹣x+10,交于C,D两点,并且OC=3BD. 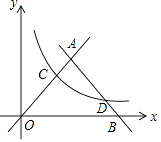
(1)求出双曲线的解析式;
(2)连结CD,求四边形OCDB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,AD=6,将矩形ABCD折叠,使得点B落在边AD上,记为点G,BC的对应边GI与边CD交于点H,折痕为EF,则AE=时,△EGH为等腰三角形. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在三角形ABC中,∠ACB=90°,∠B=50°,将此三角形绕点C沿顺时针方向旋转后得到三角形A′B′C,若点B′恰好落在线段AB上,AC、A′B′交于点O,则∠COA′的度数是( ) 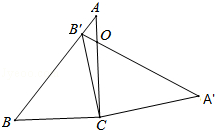
A.50°
B.60°
C.70°
D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线L1过A(0,2),B(2,0)两点,直线L2:y=mx+b过点C(1,0),且把△AOB分成两部分,其中靠近原点的那部分是一个三角形,设此三角形的面积为S,求S关于m的函数解析式,及自变量m的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com