
【题目】如图,菱形ABCD,∠A=60°,AB=4,以点B为圆心的扇形与边CD相切于点E,扇形的圆心角为60°,点E是CD的中点,图中两块阴影部分的面积分别为S1 , S2 , 则S2﹣S1= . 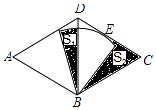
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+2的图象与反比例函数y= ![]() 的图象交于P、G两点,过点P作PA⊥x轴,一次函数图象分别交x轴、y轴于C、D两点,
的图象交于P、G两点,过点P作PA⊥x轴,一次函数图象分别交x轴、y轴于C、D两点, ![]() =
= ![]() ,且S△ADP=6.
,且S△ADP=6. 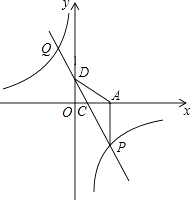
(1)求点D坐标;
(2)求一次函数和反比例函数的表达式;
(3)根据图象直接写出一次函数值小于反比例函数值时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1∶2∶1,用两个相同的管子在容器的5 cm高度处连通(即管子底离容器底5 cm),现三个容器中,只有甲中有水,水位高1 cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升![]() cm.
cm.
(1)开始注水1分钟,丙的水位上升________cm;
(2)开始注入________分钟的水量后,乙的水位比甲高0.5 cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点为M的抛物线y=a(x+1)2﹣4分别与x轴相交于点A,B(点A在点B的右侧),与y轴相交于点C(0,﹣3).
(1)求抛物线的函数表达式;
(2)判断△BCM是否为直角三角形,并说明理由.
(3)抛物线上是否存在点N(点N与点M不重合),使得以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等?若存在,求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠1=∠2,DB=DC.
(1)求证:△ABD≌△EDC;
(2)若∠A=135°,∠BDC=30°,求∠BCE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
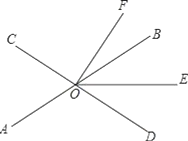
【题目】如图,直线AB、CD相交于点O,OE平分∠BOD.
(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.
①用含x的代数式表示∠EOF;
②求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个直角∠AOB,∠COD有相同的顶点O,下列结论:①∠AOC=∠BOD;
②∠AOC+∠BOD=90°;③若OC平分∠AOB,则OB平分∠COD;④∠AOD的平分线与∠COB的平分线是同一条射线. 其中正确的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司以每吨![]() 元的价格收购了
元的价格收购了![]() 吨某种药材,若直接在市场上销售,每吨的售价是
吨某种药材,若直接在市场上销售,每吨的售价是![]() 元.该公司决定加工后再出售,相关信息如下表所示:
元.该公司决定加工后再出售,相关信息如下表所示:
工艺 | 每天可加工药材的吨数 | 成品率 | 成品售价 (元/吨) |
粗加工 | 14 | 80% | 6000 |
精加工 | 6 | 60% | 11000 |
(注:①成品率80%指加工100吨原料能得到80吨可销售药材;②加工后的废品不产生效益.)
受市场影响,该公司必须在![]() 天内将这批药材加工完毕.
天内将这批药材加工完毕.
(1)若全部粗加工,可获利_______________________元;
(2)若尽可能多的精加工,剩余的直接在市场上销售,可获利_____________元;
(3)若部分粗加工,部分精加工,恰好![]() 天完成,求可获利多少元?
天完成,求可获利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com