
����Ŀ��ʵ��������ˮƽ�������мס��ҡ�������Բ��������(�����㹻��)������뾶֮��Ϊ1��2��1����������ͬ�Ĺ�����������5 cm�߶ȴ���ͨ(�����ӵ���������5 cm)����������������ֻ�м�����ˮ��ˮλ��1 cm����ͼ��ʾ����ÿ����ͬʱ���Һͱ�ע����ͬ����ˮ����ʼעˮ1�������ҵ�ˮλ����![]() cm.
cm.
(1)��ʼעˮ1����������ˮλ����________cm��
(2)��ʼע��________���ӵ�ˮ�������ҵ�ˮλ�ȼ�0.5 cm.

���𰸡� ![]()
![]() ��
��![]()
����������1�����������֪�������ұ��е�ˮ�������ȣ����ұ��ĵ�����뾶֮��Ϊ2:1�����Բ���������ʽ��������ұ���ˮλ֮�ȣ���������⣨1����
������ҵ�ˮλ�ȼ�0.5cm����Ҫ�ּ�ˮλ������ҵ�ˮλ������ӵײ�����2����ˮλ��������������ۣ��������δ֪��������ʼע��t����ˮ����������������ˮλ����ʱ����Ҫ�жϱ���ˮλ�Ƿ���ӵײ�����û��������ˮ������������г�![]() t-1=0.5�����t�������ʱ����ˮλ��������ˮλ����5���������С��5��û���������ñ���ˮ���������ˮ��������ˮλ�����������֮��Ϊ0.5cm�����г�һԪһ�η�����⼴�ɣ��ڶ����������������ҵ�ˮλ������ӵײ���ʱ�䣬�������ݼ������ߵ�ˮλ��Ϊ0.5cm�ĵ�����ϵ�г�һԪһ�η������.
t-1=0.5�����t�������ʱ����ˮλ��������ˮλ����5���������С��5��û���������ñ���ˮ���������ˮ��������ˮλ�����������֮��Ϊ0.5cm�����г�һԪһ�η�����⼴�ɣ��ڶ����������������ҵ�ˮλ������ӵײ���ʱ�䣬�������ݼ������ߵ�ˮλ��Ϊ0.5cm�ĵ�����ϵ�г�һԪһ�η������.
��1�������Һͱ�ע����ͬ����ˮ��ע��ˮ�������ͬ�������ǵĵ���뾶֮��Ϊ2:1��
����Բ���������ʽ��֪�ҡ�����ˮλ֮��Ϊ��1:4.
�ߵ�עˮ1���ӣ��ҵ�ˮλ����![]() cm��
cm��
��עˮ1���ӣ�����ˮλ����![]() ��4=
��4=![]() cm.
cm.
��2���迪ʼע��t���ӵ�ˮ�����ҵ�ˮλ�ȼ�0.5cm�������������
�ٵ���ˮλ����ʱ��
��![]() t-1=0.5��
t-1=0.5��
���t=![]() ��
��
��![]() ��
��![]() =6��5��
=6��5��
���ʱ�����������������ˮ.
��5��![]() =
=![]() �����ӣ���
�����ӣ���![]() ��
��![]() =
=![]() ��cm����������32���ӱ�������ˮ������ӵײ����ҵ�ˮλ����
��cm����������32���ӱ�������ˮ������ӵײ����ҵ�ˮλ����![]() cm��
cm��
��![]() +2��
+2��![]() (t-
(t-![]() )-1=0.5�����t=
)-1=0.5�����t=![]() .
.
�ڵ��ҵ�ˮλ������ӵײ�����ˮλ����ʱ��
���ҵ�ˮλ������ӵײ���ʱ��Ϊ��![]() +(5-
+(5-![]() )��
)��![]() ��2=
��2=![]() �����ӣ���
�����ӣ���
��5-1-2��![]() (t-
(t-![]() )=0.5��
)=0.5��
���t=![]() .
.
����������ʼעˮ![]() ��
��![]() ���Ӻ��ҵ�ˮλ�ȼ�0.5cm.
���Ӻ��ҵ�ˮλ�ȼ�0.5cm.


 ����������ϵ�д�
����������ϵ�д� �Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�
�Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
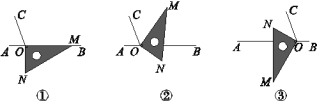
����Ŀ����ͼ����OΪֱ��AB��һ��������O������OC��ʹ��BOC��110��.��һ���dzߵ�ֱ�Ƕ�����ڵ�O��(��OMN��30��)��һ��OM������OB������һ��ON��ֱ��AB���·���
(1)��ͼ���е����dz��Ƶ�O��ʱ����ת��ͼ����ʹһ��OM�ڡ�BOC���ڲ�����ǡ��ƽ�֡�BOC�����BON�Ķ�����
(2)��ͼ���е����dz��Ƶ�O��ÿ��5�����ٶȰ���ʱ�뷽����תһ��������ת�Ĺ���������t��ʱ��ֱ��ONǡ��ƽ����ǡ�AOC����t��ֵΪ________(ֱ��д�����)��
(3)��ͼ���е����dz��Ƶ�O˳ʱ����ת��ͼ����ʹON�ڡ�AOC���ڲ�����̽����AOM���NOC��������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�Ƶ�C˳ʱ����ת90���õ�����FGCE����M��N�ֱ���BD��GE���е㣬��BC=14��CE=2����MN�ij���������

A. 7 B. 8 C. 9 D. 10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��������㳡һ��ڴ����弶�߶���ȵ�С̨�ף���̨֪���ܸ�1.5�ף�Ϊ�˰�ȫ����Ҫ��һ������ַ���AB��������FG��ֱ�ҳ�Ϊ1�IJ���ּܸ�AD��BC�����ӵĵ˷ֱ�ΪD��C�����ҡ�DAB=66.5�㣮���ο����ݣ�cos66.5���0.40��sin66.5���0.92�� 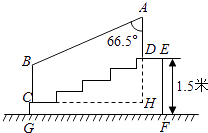
��1�����D���C�ĸ߶Ȳ�DH��
��2�������в���ֲ��ϵ��ܳ��ȣ���AD+AB+BC�ij��������ȷ��0.1�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�
����߳�Ϊ![]() ��С��������ͼ�ٷ��ã�Ҫ���������߶ν����Ƿָ�������ֺ������ƴ�ӳ�һ���µ������Σ�
��С��������ͼ�ٷ��ã�Ҫ���������߶ν����Ƿָ�������ֺ������ƴ�ӳ�һ���µ������Σ�



С��������˼���ģ�ͼ��������߳�Ϊ![]() ��С�����ε�����ĺ�Ϊ
��С�����ε�����ĺ�Ϊ![]() ��ƴ�Ӻ�������ε����ҲӦ����
��ƴ�Ӻ�������ε����ҲӦ����![]() ���ʶ�ƴ�Ӻ�������εı߳�Ϊ
���ʶ�ƴ�Ӻ�������εı߳�Ϊ![]() ������뵽�����ݹ��ɶ��������쳤Ϊ
������뵽�����ݹ��ɶ��������쳤Ϊ![]() ���߶Σ�����
���߶Σ�����![]() ������뵽����ֱ�DZ߷ֱ�Ϊ
������뵽����ֱ�DZ߷ֱ�Ϊ![]() ��
��![]() ��ֱ�������ε�б��������
��ֱ�������ε�б��������![]() ����ͼ�ڣ�����ƴ�ӳ���һ���㳤Ϊ
����ͼ�ڣ�����ƴ�ӳ���һ���㳤Ϊ![]() �������Σ�
��������
�ο�����IJ��Ϻ�С����˼��������������⣺
��![]() ������߳�Ϊ
������߳�Ϊ![]() ��С��������ͼ�ܷ��ã�����ͼ�ۣ���ͼ���л����ָ��ߺ�ƴ�Ӻ�������Σ�ֻҪ����һ�ּ��ɣ���
��С��������ͼ�ܷ��ã�����ͼ�ۣ���ͼ���л����ָ��ߺ�ƴ�Ӻ�������Σ�ֻҪ����һ�ּ��ɣ���
��![]() ��ʮ���߳�Ϊ
��ʮ���߳�Ϊ![]() ��С��������ͼ�ݷ��ã�����ͼ�ۣ���ͼ���л��������ָ��߽����Ƿָ�������֣�������ƴ�Ӻ�������Σ�ֻҪ����һ�ּ��ɣ���
��С��������ͼ�ݷ��ã�����ͼ�ۣ���ͼ���л��������ָ��߽����Ƿָ�������֣�������ƴ�Ӻ�������Σ�ֻҪ����һ�ּ��ɣ���
��![]() ������߳�Ϊ
������߳�Ϊ![]() ��С��������ͼ���ã�����ͼ�ۣ���ͼ���л��������ָ��߽����Ƿָ�������֣�������ƴ�Ӻ�������Σ�ֻҪ����һ�ּ��ɣ���
��С��������ͼ���ã�����ͼ�ۣ���ͼ���л��������ָ��߽����Ƿָ�������֣�������ƴ�Ӻ�������Σ�ֻҪ����һ�ּ��ɣ���



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����C���߶�AB�ϣ�AC=6cm��MB=10cm����M��N�ֱ�ΪAC��BC���е㣮
![]()
��1�����߶�BC�ij���
��2�����߶�MN�ij���
��3����C���߶�AB�ӳ����ϣ�������AC��BC=b cm��M��N�ֱ����߶�AC��BC���е㣬���ܲ���MN�ij�������д����Ľ��ۣ�����Ҫ˵�����ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y=��ax+b��ͼ���뷴��������y= ![]() ��ͼ���ཻ�ڵ�A����4����2����B��m��4������y���ཻ�ڵ�C��
��ͼ���ཻ�ڵ�A����4����2����B��m��4������y���ཻ�ڵ�C�� 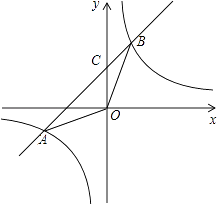
��1������������һ�κ����ı���ʽ��
��2�����C�����꼰��AOB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD����A=60�㣬AB=4���Ե�BΪԲ�ĵ��������CD�����ڵ�E�����ε�Բ�Ľ�Ϊ60�㣬��E��CD���е㣬ͼ��������Ӱ���ֵ�����ֱ�ΪS1 �� S2 �� ��S2��S1= �� 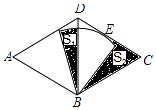
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com