
【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣ax+b的图象与反比例函数y= ![]() 的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C.
的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C. 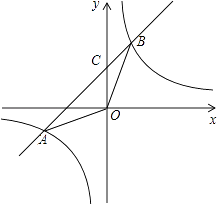
(1)求反比例函数和一次函数的表达式;
(2)求点C的坐标及△AOB的面积.
【答案】
(1)解:∵点A(﹣4,﹣2)在反比例函数y= ![]() 的图象上,
的图象上,
∴k=﹣4×(﹣2)=8,
∴反比例函数的表达式为y= ![]() ;
;
∵点B(m,4)在反比例函数y= ![]() 的图象上,
的图象上,
∴4m=8,解得:m=2,
∴点B(2,4).
将点A(﹣4,﹣2)、B(2,4)代入y=﹣ax+b中,
得: ![]() ,解得:
,解得: ![]() ,
,
∴一次函数的表达式为y=x+2
(2)解:令y=x+2中x=0,则y=2,
∴点C的坐标为(0,2).
∴S△AOB= ![]() OC×(xB﹣xA)=
OC×(xB﹣xA)= ![]() ×2×[2﹣(﹣4)]=6.
×2×[2﹣(﹣4)]=6.
【解析】(1)由点A的坐标利用反比例函数图象上点的坐标特征即可求出k值,从而得出反比例函数表达式,再由点B的坐标和反比例函数表达式即可求出m值,结合点A、B的坐标利用待定系数法即可求出一次函数表达式;(2)令一次函数表达式中x=0求出y值即可得出点C的坐标,利用分解图形求面积法结合点A、B的坐标即可得出结论.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( ) 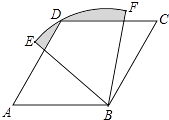
A.![]() ﹣
﹣ ![]() ??
??
B.![]() ﹣
﹣ ![]() ??
??
C.π﹣ ![]() ??
??
D.π﹣ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位运动员在一段2000米长的笔直公路上进行跑步比赛,比赛开始时甲在起点,乙在甲的前面200米,他们同时同向出发匀速前进,甲的速度是8米/秒,乙的速度是6米/秒,先到终点者在终点原地等待.设甲、乙两人之间的距离是y米,比赛时间是x秒,当两人都到达终点计时结束,整个过程中y与之间的函数图象是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1∶2∶1,用两个相同的管子在容器的5 cm高度处连通(即管子底离容器底5 cm),现三个容器中,只有甲中有水,水位高1 cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升![]() cm.
cm.
(1)开始注水1分钟,丙的水位上升________cm;
(2)开始注入________分钟的水量后,乙的水位比甲高0.5 cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校在落实国家“营养餐”工程中,选用了A,B,C,D种不同类型的套餐.实行一段时间后,学校决定在全校范围内随机抽取部分学生对“你喜欢的套餐类型(必选且只选一种)”进行问卷调查,将调查情况整理后,绘制成如图所示的两个统计图. 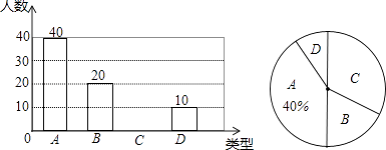
请你根据以上信息解答下列问题:
(1)在这次调查中,一共抽取了名学生;
(2)请补全条形统计图;
(3)如果全校有1200名学生,请你估计其中喜欢D套餐的学生的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点为M的抛物线y=a(x+1)2﹣4分别与x轴相交于点A,B(点A在点B的右侧),与y轴相交于点C(0,﹣3).
(1)求抛物线的函数表达式;
(2)判断△BCM是否为直角三角形,并说明理由.
(3)抛物线上是否存在点N(点N与点M不重合),使得以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等?若存在,求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠1=∠2,DB=DC.
(1)求证:△ABD≌△EDC;
(2)若∠A=135°,∠BDC=30°,求∠BCE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个直角∠AOB,∠COD有相同的顶点O,下列结论:①∠AOC=∠BOD;
②∠AOC+∠BOD=90°;③若OC平分∠AOB,则OB平分∠COD;④∠AOD的平分线与∠COB的平分线是同一条射线. 其中正确的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2﹣2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A、B,点A坐标为(4,0).
(1)求该抛物线的解析式;
(2)抛物线的顶点为N,在x轴上找一点K,使CK+KN最小,并求出点K的坐标;
(3)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;
(4)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com