
【题目】某学校在落实国家“营养餐”工程中,选用了A,B,C,D种不同类型的套餐.实行一段时间后,学校决定在全校范围内随机抽取部分学生对“你喜欢的套餐类型(必选且只选一种)”进行问卷调查,将调查情况整理后,绘制成如图所示的两个统计图. 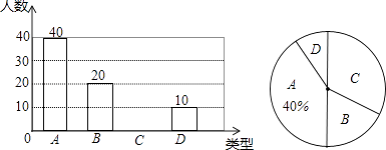
请你根据以上信息解答下列问题:
(1)在这次调查中,一共抽取了名学生;
(2)请补全条形统计图;
(3)如果全校有1200名学生,请你估计其中喜欢D套餐的学生的人数.
科目:初中数学 来源: 题型:
【题目】某校在“6·26国际禁毒日”前组织七年级全体学生320人进行了一次“毒品预防知识”竞赛,赛后随机抽取了部分学生成绩进行统计,制作了频数分布表和频数分布直方图.请根据图表中提供的信息,解答下列问题:


(1)表中![]() =___,
=___, ![]() =____,并补全直方图;
=____,并补全直方图;
(2)若用扇形统计图描述此成绩统计分布情况,则分数段80≤![]() <100对应扇形的圆心角度数是___;
<100对应扇形的圆心角度数是___;
(3)请估计该年级分数在60≤![]() <70的学生有多少人?
<70的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b(k≠0)和反比例函数y2= ![]() (m≠0)的图象交于点A(﹣1,6),B(a,﹣2).
(m≠0)的图象交于点A(﹣1,6),B(a,﹣2). 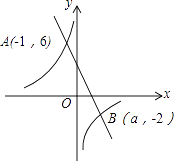
(1)求一次函数与反比例函数的解析式;
(2)根据图象直接写出y1>y2时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
五个边长为![]() 的小正方形如图①放置,要求用两条线段将它们分割成三部分后把它们拼接成一个新的正方形.
的小正方形如图①放置,要求用两条线段将它们分割成三部分后把它们拼接成一个新的正方形.



小辰是这样思考的:图①中五个边长为![]() 的小正方形的面积的和为
的小正方形的面积的和为![]() ,拼接后的正方形的面积也应该是
,拼接后的正方形的面积也应该是![]() ,故而拼接后的正方形的边长为
,故而拼接后的正方形的边长为![]() ,因此想到了依据勾股定理,构造长为
,因此想到了依据勾股定理,构造长为![]() 的线段,即:
的线段,即:![]() ,因此想到了两直角边分别为
,因此想到了两直角边分别为![]() 和
和![]() 的直角三角形的斜边正好是
的直角三角形的斜边正好是![]() ,如图②,进而拼接成了一个便长为
,如图②,进而拼接成了一个便长为![]() 的正方形.
的正方形.
参考上面的材料和小辰的思考方法,解决问题:
(![]() )五个边长为
)五个边长为![]() 的小正方形如图④放置,类似图③,在图④中画出分割线和拼接后的正方形(只要画出一种即可).
的小正方形如图④放置,类似图③,在图④中画出分割线和拼接后的正方形(只要画出一种即可).
(![]() )十个边长为
)十个边长为![]() 的小正方形如图⑤放置,类似图③,在图⑤中画出两条分割线将它们分割成三部分,并画出拼接后的正方形(只要画出一种即可).
的小正方形如图⑤放置,类似图③,在图⑤中画出两条分割线将它们分割成三部分,并画出拼接后的正方形(只要画出一种即可).
(![]() )五个边长为
)五个边长为![]() 的小正方形如图⑥放置,类似图③,在图⑥中画出两条分割线将它们分割成三部分,并画出拼接后的正方形(只要画出一种即可).
的小正方形如图⑥放置,类似图③,在图⑥中画出两条分割线将它们分割成三部分,并画出拼接后的正方形(只要画出一种即可).



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在长方形ABCD中,AB=12 cm,BC=6 cm.点P沿AB边从点A开始向点B以2 cm/s的速度移动;点Q沿DA边从点D开始向点A以1 cm/s的速度移动.
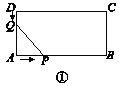
设点P,Q同时出发,用t(s)表示移动的时间.
(发现) DQ=________cm,AP=________cm.(用含t的代数式表示)
(拓展)(1)如图①,当t=________s时,线段AQ与线段AP相等?
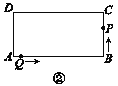
(2)如图②,点P,Q分别到达B,A后继续运动,点P到达点C后都停止运动.
当t为何值时,AQ=![]() CP?
CP?
(探究)若点P,Q分别到达点B,A后继续沿着A—B—C—D—A的方向运动,当点P与点Q第一次相遇时,请直接写出相遇点的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣ax+b的图象与反比例函数y= ![]() 的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C.
的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C. 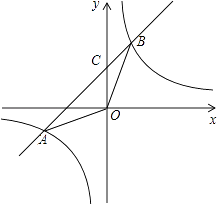
(1)求反比例函数和一次函数的表达式;
(2)求点C的坐标及△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”假期,成都某公司组织部分员工分别到甲、乙、丙、丁四地考察,公司按定额购买了前往各地的车票,如图是用来制作完整的车票种类和相应数量的条形统计图,根据统计图回答下列问题:
![]() 若去丙地的车票占全部车票的
若去丙地的车票占全部车票的![]() ,则总票数为______ 张,去丁地的车票有______ 张
,则总票数为______ 张,去丁地的车票有______ 张![]()
![]() 若公司采用随机抽取的方式发车票,小胡先从所有的车票中随机抽取一张
若公司采用随机抽取的方式发车票,小胡先从所有的车票中随机抽取一张![]() 所有车票的形状、大小、质地完全相同、均匀
所有车票的形状、大小、质地完全相同、均匀![]() ,那么员工小胡抽到去甲地的车票的概率是多少?
,那么员工小胡抽到去甲地的车票的概率是多少?
![]() 若有一张车票,小王和小李都想要,他们决定采取掷一枚质地均匀的正方体骰子的方式来确定给谁,其上的数字是3的倍数,则给小王,否则给小李
若有一张车票,小王和小李都想要,他们决定采取掷一枚质地均匀的正方体骰子的方式来确定给谁,其上的数字是3的倍数,则给小王,否则给小李![]() 请问这个规则对双方是否公平?若公平请说明理由;若不公平,请通过计算说明对谁更有利.
请问这个规则对双方是否公平?若公平请说明理由;若不公平,请通过计算说明对谁更有利.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组想利用所学的知识了解某广告牌的高度(图中GH的长),经测量知CD=2m,在B处测得点D的仰角为60°,在A处测得点C的仰角为30°,AB=10m,且A、B、H三点共线,请根据以上数据计算GH的长( ![]() ,要求结果精确得到0.1m)
,要求结果精确得到0.1m)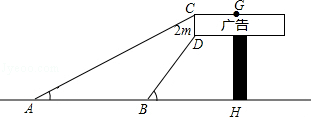
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点D的对应点D′.
(1)根据特征画出平移后的△A′B′C′;
(2)利用网格的特征,画出AC边上的高BE并标出画法过程中的特征点;
(3)△A′B′C′的面积为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com