
【题目】如图,顶点为M的抛物线y=a(x+1)2﹣4分别与x轴相交于点A,B(点A在点B的右侧),与y轴相交于点C(0,﹣3).
(1)求抛物线的函数表达式;
(2)判断△BCM是否为直角三角形,并说明理由.
(3)抛物线上是否存在点N(点N与点M不重合),使得以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等?若存在,求出点N的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵抛物线y=a(x+1)2﹣4与y轴相交于点C(0,﹣3).
∴﹣3=a﹣4,
∴a=1,
∴抛物线解析式为y=(x+1)2﹣4=x2+2x﹣3
(2)
解:△BCM是直角三角形
理由:由(1)有,抛物线解析式为y=(x+1)2﹣4,
∵顶点为M的抛物线y=a(x+1)2﹣4,
∴M(﹣1,﹣4),
由(1)抛物线解析式为y=x2+2x﹣3,
令y=0,
∴x2+2x﹣3=0,
∴x1=﹣3,x2=1,
∴A(1,0),B(﹣3,0),
∴BC2=9+9=18,CM2=1+1=2,BM2=4+14=20,
∴BC2+CM2=BM2,
∴△BCM是直角三角形
(3)
解:存在,N(﹣1+ ![]() ,
, ![]() )或N(﹣1﹣
)或N(﹣1﹣ ![]() ,
, ![]() ),
),
∵以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等,且点M是抛物线的顶点,
∴①点N在x轴上方的抛物线上,
如图,
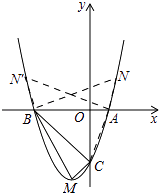
由(2)有△BCM是直角三角形,BC2=18,CM2=2,
∴BC=3 ![]() ,CM=
,CM= ![]() ,
,
∴S△BCM= ![]() BC×CM=
BC×CM= ![]() ×3
×3 ![]() ×
× ![]() =3,
=3,
设N(m,n),
∵以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等,
∴S△ABN+S△ABC=S△BCM+S△ABC,
∴S△ABN=S△BCM=3,
∵A(1,0),B(﹣3,0),
∴AB=4,
∴S△ABN= ![]() ×AB×n=
×AB×n= ![]() ×4×n=2n=3,
×4×n=2n=3,
∴n= ![]() ,
,
∵N在抛物线解析式为y=x2+2x﹣3的图象上,
∴m2+2m﹣3= ![]() ,
,
∴m1=﹣1+ ![]() ,m2=﹣1﹣
,m2=﹣1﹣ ![]() ,
,
∴N(﹣1+ ![]() ,
, ![]() )或N(﹣1﹣
)或N(﹣1﹣ ![]() ,
, ![]() ).
).
②如图2,
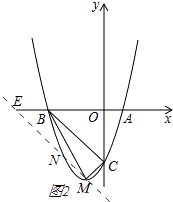
②点N在x轴下方的抛物线上,
∵点C在对称轴的右侧,
∴点N在对称轴右侧不存在,只有在对称轴的左侧,
过点M作MN∥BC,交抛物线于点N,
∵B(﹣3,0),C(0,﹣3),
∴直线BC解析式为y=﹣x﹣3,
设MN的解析式为y=﹣x+b
∵抛物线解析式为y=(x+1)2﹣4①,
∴M(﹣1,﹣4),
∴直线MN解析式为y=﹣x﹣5②,
联立①②得 ![]() (舍),
(舍), ![]() ,
,
∴N(﹣2,﹣3),
即:N(﹣1+ ![]() ,
, ![]() )或N(﹣1﹣
)或N(﹣1﹣ ![]() ,
, ![]() )或N(﹣2,﹣3)
)或N(﹣2,﹣3)
【解析】(1)用待定系数法求出抛物线解析式即可;(2)由抛物线解析式确定出抛物线的顶点坐标和与x轴的交点坐标,用勾股定理的逆定理即可;(3)根据题意判断出点N只能在x轴上方的抛物线上,由已知四边形的面积相等转化出S△ABN=S△BCM , 然后求出三角形BCM的面积,再建立关于点N的坐标的方程求解即可.


科目:初中数学 来源: 题型:
【题目】在数-5,1,-3,5,-2中任取三个数相乘,其中最大的积是a,最小的积是b.
(1)求a,b的值;
(2)若|x+a|+|y-b|=0,求(x+y)÷(x-y)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某城市市民广场一入口处有五级高度相等的小台阶.已知台阶总高1.5米,为了安全,现要做一个不锈钢扶手AB及两根与FG垂直且长为1米的不锈钢架杆AD和BC(杆子的底端分别为D、C),且∠DAB=66.5°.(参考数据:cos66.5°≈0.40,sin66.5°≈0.92) 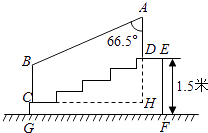
(1)求点D与点C的高度差DH;
(2)求所有不锈钢材料的总长度(即AD+AB+BC的长,结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,AC=6cm,MB=10cm,点M、N分别为AC、BC的中点.
![]()
(1)求线段BC的长;
(2)求线段MN的长;
(3)若C在线段AB延长线上,且满足AC﹣BC=b cm,M,N分别是线段AC,BC的中点,你能猜想MN的长度吗?请写出你的结论(不需要说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣ax+b的图象与反比例函数y= ![]() 的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C.
的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C. 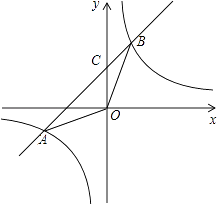
(1)求反比例函数和一次函数的表达式;
(2)求点C的坐标及△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,补充条件后仍不一定能保证△ABC≌△A′B′C′,则补充的这个条件是( )

A. BC=B′C′ B. ∠A=∠A′ C. AC=A′C′ D. ∠C=∠C′
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD,∠A=60°,AB=4,以点B为圆心的扇形与边CD相切于点E,扇形的圆心角为60°,点E是CD的中点,图中两块阴影部分的面积分别为S1 , S2 , 则S2﹣S1= . 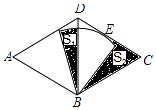
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角形的直角三角板的直角顶点放在点O处.
(1)如图1,将三角板MON的一边ON与射线OB重合,则∠MOC=___________;
(2)如图2,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON和∠CON的度数;

(3)将三角板MON绕点O逆时针旋转至图3时,∠NOC=![]() ∠AOM,求∠NOB的度数.
∠AOM,求∠NOB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现与探索。
(1)根据小明的解答将下列各式因式分解

① a2-12a+20;②(a-1)2-8(a-1)+7;③ a2-6ab+5b2
(2)根据小丽的思考解决下列问题:

①说明:代数式a2-12a+20的最小值为-16.
②请仿照小丽的思考解释代数式-(a+1)2+8的最大值为8,并求代数式-a2+12a-8的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com