练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在四边形ABCD中，AB∥CD，∠1=∠2，DB=DC．

    （1）求证：△ABD≌△EDC；

    （2）若∠A=135°，∠BDC=30°，求∠BCE的度数．

    【答案】（1）证明见解析；（2）60°．

    【解析】试题分析：由全等三角形的判定方法：ASA，即可证明：△ABD≌△EDC；

    （2）根据三角形内角和定理可求出∠1的度数，进而可得到∠2的度数，再根据△BDC是等腰三角形，即可求出∠BCE的度数．

    试题解析：（1）证明：∵AB∥CD，∴∠ABD=∠EDC，

    在△ABD和△EDC中，， ∴△ABD≌△EDC（ASA），

    （2）解：∵∠ABD=∠EDC=30°，∠A=135°， ∴∠1=∠2=15°， ∵DB=DC，

    ∴∠DCB=(180°－∠DBC)=75°， ∴∠BCE=75°﹣15°=60°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，点M，N分别在正三角形ABC的BC，CA边上，且BM=CN，AM，BN交于点Q．求证：∠BQM=60°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料：

    五个边长为的小正方形如图①放置，要求用两条线段将它们分割成三部分后把它们拼接成一个新的正方形．

    小辰是这样思考的：图①中五个边长为的小正方形的面积的和为，拼接后的正方形的面积也应该是，故而拼接后的正方形的边长为，因此想到了依据勾股定理，构造长为的线段，即：，因此想到了两直角边分别为和的直角三角形的斜边正好是，如图②，进而拼接成了一个便长为的正方形．

    参考上面的材料和小辰的思考方法，解决问题：

    （）五个边长为的小正方形如图④放置，类似图③，在图④中画出分割线和拼接后的正方形（只要画出一种即可）．

    （）十个边长为的小正方形如图⑤放置，类似图③，在图⑤中画出两条分割线将它们分割成三部分，并画出拼接后的正方形（只要画出一种即可）．

    （）五个边长为的小正方形如图⑥放置，类似图③，在图⑥中画出两条分割线将它们分割成三部分，并画出拼接后的正方形（只要画出一种即可）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，一次函数y=﹣ax+b的图象与反比例函数y= 的图象相交于点A（﹣4，﹣2），B（m，4），与y轴相交于点C．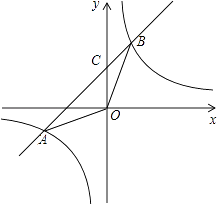
    （1）求反比例函数和一次函数的表达式；
    （2）求点C的坐标及△AOB的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“五一”假期，成都某公司组织部分员工分别到甲、乙、丙、丁四地考察，公司按定额购买了前往各地的车票，如图是用来制作完整的车票种类和相应数量的条形统计图，根据统计图回答下列问题：

    若去丙地的车票占全部车票的，则总票数为______ 张，去丁地的车票有______ 张

    若公司采用随机抽取的方式发车票，小胡先从所有的车票中随机抽取一张所有车票的形状、大小、质地完全相同、均匀，那么员工小胡抽到去甲地的车票的概率是多少？

    若有一张车票，小王和小李都想要，他们决定采取掷一枚质地均匀的正方体骰子的方式来确定给谁，其上的数字是3的倍数，则给小王，否则给小李请问这个规则对双方是否公平？若公平请说明理由；若不公平，请通过计算说明对谁更有利．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，菱形ABCD，∠A=60°，AB=4，以点B为圆心的扇形与边CD相切于点E，扇形的圆心角为60°，点E是CD的中点，图中两块阴影部分的面积分别为S1 ， S2 ， 则S2﹣S1= ．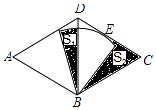

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数学兴趣小组想利用所学的知识了解某广告牌的高度（图中GH的长），经测量知CD=2m，在B处测得点D的仰角为60°，在A处测得点C的仰角为30°，AB=10m，且A、B、H三点共线，请根据以上数据计算GH的长（ ，要求结果精确得到0.1m）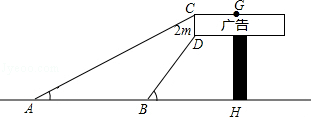

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列说法：①2a+b=0，②当﹣1≤x≤3时，y＜0；③3a+c=0；④若（x1 ， y1）（x2、y2）在函数图象上，当0＜x1＜x2时，y1＜y2 ， 其中正确的是（ ）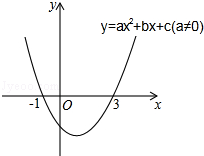
    A.①②④
    B.①③
    C.①②③
    D.①③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，过等边三角形ABC边AB上一点D作DE∥BC交边AC于点E，分别取BC，DE的中点M，N，连接MN．

    （1）发现：在图1中， =；

    （2）应用：如图2，将△ADE绕点A旋转，请求出 的值；

    （3）拓展：如图3，△ABC和△ADE是等腰三角形，且∠BAC=∠DAE，M，N分别是底边BC，DE的中点，若BD⊥CE，请直接写出 的值．

    查看答案和解析>>

    同步练习册答案