
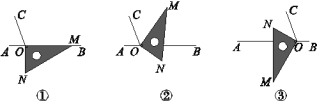
【题目】如图①,O为直线AB上一点,过点O作射线OC,使∠BOC=110°.将一三角尺的直角顶点放在点O处(∠OMN=30°),一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图①中的三角尺绕点O逆时针旋转至图②,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠BON的度数;
(2)将图①中的三角尺绕点O以每秒5°的速度按逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为________(直接写出结果);
(3)将图①中的三角尺绕点O顺时针旋转至图③,使ON在∠AOC的内部,请探究∠AOM与∠NOC的数量关系,并说明理由.
【答案】(1) 35°;(2) 11或47;(3)见解析.
【解析】
(1)根据角平分线的定义以及直角的定义,即可求得∠BON的度数;
(2)分两种情况:ON的反向延长线平分∠AOC或射线ON平分∠AOC,分别根据角平分线的定义以及角的和差关系进行计算即可;
(3)根据∠MON=90°,∠AOC=70°,分别求得∠AOM=90°-∠AON,∠NOC=70°-∠AON,再根据∠AOM-∠NOC=(90°-∠AON)-(70°-∠AON)进行计算,即可得出∠AOM与∠NOC的数量关系.
(1)如图2,
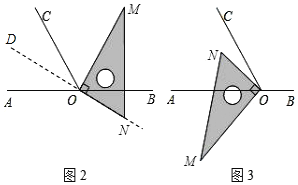
∵OM平分∠BOC,
∴∠MOC=∠MOB,
又∵∠BOC=110°,
∴∠MOB=55°,
∵∠MON=90°,
∴∠BON=∠MON-∠MOB=35°;
(2)分两种情况:
①如图2,∵∠BOC=110°
∴∠AOC=70°,
当直线ON恰好平分锐角∠AOC时,∠AOD=∠COD=35°,
∴∠BON=35°,∠BOM=55°,
即逆时针旋转的角度为55°,
由题意得,5t=55°
解得t=11(s);
②如图3,当NO平分∠AOC时,∠NOA=35°,
∴∠AOM=55°,
即逆时针旋转的角度为:180°+55°=235°,
由题意得,5t=235°,
解得t=47(s),
综上所述,t=11s或47s时,直线ON恰好平分锐角∠AOC;
故答案为:11或47;
(3)∠AOM-∠NOC=20°.
理由:∵∠MON=90°,∠AOC=70°,
∴∠AOM=90°-∠AON,∠NOC=70°-∠AON,
∴∠AOM-∠NOC=(90°-∠AON)-(70°-∠AON)=20°,
∴∠AOM与∠NOC的数量关系为:∠AOM-∠NOC=20°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,点E,点F分别在菱形ABCD的边AB,AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于H,若 ![]() =2,则
=2,则 ![]() 的值为( )
的值为( ) 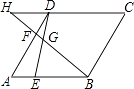
A.![]() ??
??
B.![]() ??
??
C.![]() ??
??
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有两枚质地均匀的正方体骰子,每枚骰子的六个面上都分别标有数字1、2、3、4、5、6.同时投掷这两枚骰子,以朝上一面所标的数字为掷得的结果,那么所得结果之和为9的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO,已知BD=![]() .
.
(1)求正方形ABCD的边长;
(2)求OE的长;
(3)①求证:CN=AF;
②直接写出四边形AFBO的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间. 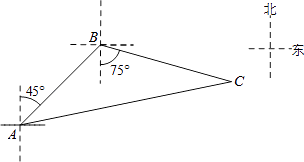
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设点A(x1 , y1)和点B(x2 , y2)是反比例函数y= ![]() 图象上的两点,当x1<x2<0时,y1>y2 , 则一次函数y=﹣2x+k的图象不经过的象限是( )
图象上的两点,当x1<x2<0时,y1>y2 , 则一次函数y=﹣2x+k的图象不经过的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( ) 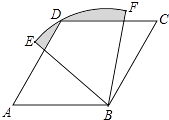
A.![]() ﹣
﹣ ![]() ??
??
B.![]() ﹣
﹣ ![]() ??
??
C.π﹣ ![]() ??
??
D.π﹣ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+2的图象与反比例函数y= ![]() 的图象交于P、G两点,过点P作PA⊥x轴,一次函数图象分别交x轴、y轴于C、D两点,
的图象交于P、G两点,过点P作PA⊥x轴,一次函数图象分别交x轴、y轴于C、D两点, ![]() =
= ![]() ,且S△ADP=6.
,且S△ADP=6. 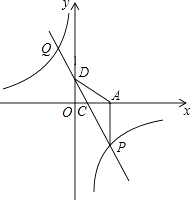
(1)求点D坐标;
(2)求一次函数和反比例函数的表达式;
(3)根据图象直接写出一次函数值小于反比例函数值时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1∶2∶1,用两个相同的管子在容器的5 cm高度处连通(即管子底离容器底5 cm),现三个容器中,只有甲中有水,水位高1 cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升![]() cm.
cm.
(1)开始注水1分钟,丙的水位上升________cm;
(2)开始注入________分钟的水量后,乙的水位比甲高0.5 cm.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com