
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间. 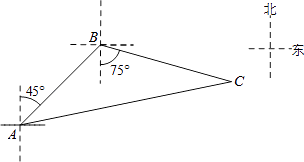
【答案】解:设巡逻船从出发到成功拦截所用时间为x小时;如图所示, 
由题意得:∠ABC=45°+75°=120°,AB=12,BC=10x,AC=14x,
过点A作AD⊥CB的延长线于点D,
在Rt△ABD中,AB=12,∠ABD=60°,
∴BD=ABcos60°= ![]() AB=6,AD=ABsin60°=6
AB=6,AD=ABsin60°=6 ![]() ,
,
∴CD=10x+6.
在Rt△ACD中,由勾股定理得: ![]() ,
,
解得: ![]() (不合题意舍去).
(不合题意舍去).
答:巡逻船从出发到成功拦截所用时间为2小时
【解析】设巡逻船从出发到成功拦截所用时间为x小时,由题意得出∠ABC=120°,AB=12,BC=10x,AC=14x,过点A作AD⊥CB的延长线于点D,在Rt△ABD中,由三角函数得出BD、AD的长度,得出CD=10x+6.在Rt△ACD中,由勾股定理得出方程,解方程即可.


科目:初中数学 来源: 题型:
【题目】如图,BE是AB的延长线,指出下面各组中的两个角是由哪两条直线被哪一条直线所截形成的?它们是什么角?
(1)∠A和∠D;
(2)∠A和∠CBA;
(3)∠C和∠CBE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD= ![]() ,CD=
,CD= ![]() ,点P是四边形ABCD四条边上的一个动点,若P到BD的距离为
,点P是四边形ABCD四条边上的一个动点,若P到BD的距离为 ![]() ,则满足条件的点P有个.
,则满足条件的点P有个. 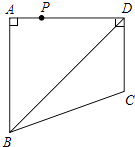
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,∠BOM=90°,∠DON=90°.
(1)若∠COM=∠AOC,求∠AOD的度数;
(2)若∠COM=![]() ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F. 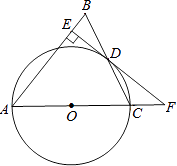
(1)求证:EF是⊙O的切线;
(2)若EB= ![]() ,且sin∠CFD=
,且sin∠CFD= ![]() ,求⊙O的半径与线段AE的长.
,求⊙O的半径与线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,O为直线AB上一点,过点O作射线OC,使∠BOC=110°.将一三角尺的直角顶点放在点O处(∠OMN=30°),一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图①中的三角尺绕点O逆时针旋转至图②,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠BON的度数;
(2)将图①中的三角尺绕点O以每秒5°的速度按逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为________(直接写出结果);
(3)将图①中的三角尺绕点O顺时针旋转至图③,使ON在∠AOC的内部,请探究∠AOM与∠NOC的数量关系,并说明理由.
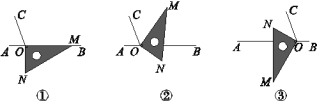
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在“6·26国际禁毒日”前组织七年级全体学生320人进行了一次“毒品预防知识”竞赛,赛后随机抽取了部分学生成绩进行统计,制作了频数分布表和频数分布直方图.请根据图表中提供的信息,解答下列问题:


(1)表中![]() =___,
=___, ![]() =____,并补全直方图;
=____,并补全直方图;
(2)若用扇形统计图描述此成绩统计分布情况,则分数段80≤![]() <100对应扇形的圆心角度数是___;
<100对应扇形的圆心角度数是___;
(3)请估计该年级分数在60≤![]() <70的学生有多少人?
<70的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
五个边长为![]() 的小正方形如图①放置,要求用两条线段将它们分割成三部分后把它们拼接成一个新的正方形.
的小正方形如图①放置,要求用两条线段将它们分割成三部分后把它们拼接成一个新的正方形.



小辰是这样思考的:图①中五个边长为![]() 的小正方形的面积的和为
的小正方形的面积的和为![]() ,拼接后的正方形的面积也应该是
,拼接后的正方形的面积也应该是![]() ,故而拼接后的正方形的边长为
,故而拼接后的正方形的边长为![]() ,因此想到了依据勾股定理,构造长为
,因此想到了依据勾股定理,构造长为![]() 的线段,即:
的线段,即:![]() ,因此想到了两直角边分别为
,因此想到了两直角边分别为![]() 和
和![]() 的直角三角形的斜边正好是
的直角三角形的斜边正好是![]() ,如图②,进而拼接成了一个便长为
,如图②,进而拼接成了一个便长为![]() 的正方形.
的正方形.
参考上面的材料和小辰的思考方法,解决问题:
(![]() )五个边长为
)五个边长为![]() 的小正方形如图④放置,类似图③,在图④中画出分割线和拼接后的正方形(只要画出一种即可).
的小正方形如图④放置,类似图③,在图④中画出分割线和拼接后的正方形(只要画出一种即可).
(![]() )十个边长为
)十个边长为![]() 的小正方形如图⑤放置,类似图③,在图⑤中画出两条分割线将它们分割成三部分,并画出拼接后的正方形(只要画出一种即可).
的小正方形如图⑤放置,类似图③,在图⑤中画出两条分割线将它们分割成三部分,并画出拼接后的正方形(只要画出一种即可).
(![]() )五个边长为
)五个边长为![]() 的小正方形如图⑥放置,类似图③,在图⑥中画出两条分割线将它们分割成三部分,并画出拼接后的正方形(只要画出一种即可).
的小正方形如图⑥放置,类似图③,在图⑥中画出两条分割线将它们分割成三部分,并画出拼接后的正方形(只要画出一种即可).



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com