
【题目】如图,在△ABC中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F. 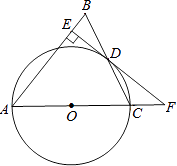
(1)求证:EF是⊙O的切线;
(2)若EB= ![]() ,且sin∠CFD=
,且sin∠CFD= ![]() ,求⊙O的半径与线段AE的长.
,求⊙O的半径与线段AE的长.
【答案】
(1)证明:连结OD,如图,
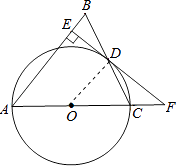
∵AB=AC,
∴∠B=∠ACD,
∵OC=OD,
∴∠ODC=∠OCD,
∴∠B=∠ODC,
∴OD∥AB,
∵DE⊥AB,
∴OD⊥EF,
∴EF是⊙O的切线
(2)解:在Rt△ODF,sin∠OFD= ![]() =
= ![]() ,
,
设OD=3x,则OF=5x,
∴AB=AC=6x,AF=8x,
在Rt△AEF中,∵sin∠AFE= ![]() =
= ![]() ,
,
∴AE= ![]() 8x=
8x= ![]() x,
x,
∵BE=AB﹣AE=6x﹣ ![]() x=
x= ![]() x,
x,
∴ ![]() x=
x= ![]() ,解得x=
,解得x= ![]() ,
,
∴AE= ![]()
![]() =6,
=6,
OD=3 ![]() =
= ![]() ,
,
即⊙O的半径长为 ![]() .
.
【解析】(1)连结OD,如图,由AB=AC得到∠B=∠ACD,由OC=OD得到∠ODC=∠OCD,则∠B=∠ODC,于是可判断OD∥AB,然后利用DE⊥AB得到OD⊥EF,然后根据切线的判定定理得到结论;(2)在Rt△ODF利用正弦的定义得到sin∠OFD= ![]() =
= ![]() ,则可设OD=3x,OF=5x,所以AB=AC=6x,AF=8x,在Rt△AEF中由于sin∠AFE=
,则可设OD=3x,OF=5x,所以AB=AC=6x,AF=8x,在Rt△AEF中由于sin∠AFE= ![]() =
= ![]() ,可得到AE=
,可得到AE= ![]() x,接着表示出BE得到
x,接着表示出BE得到 ![]() x=
x= ![]() ,解得x=
,解得x= ![]() ,于是可得到AE和OD的长.
,于是可得到AE和OD的长.
【考点精析】掌握切线的判定定理是解答本题的根本,需要知道切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】如图,点P与点 Q 都在y轴上,且关于x轴对称.
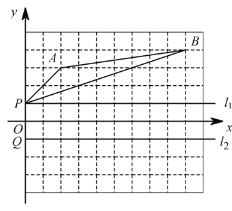
(1)请画出△ABP 关于x轴的对称图形 ![]() (其中点 A 的对称点用
(其中点 A 的对称点用 ![]() 表示,点 的对称点用
表示,点 的对称点用 ![]() 表示);
表示);
(2)点P ,Q 同时都从y轴上的位置出发,分别沿l1,l2方向,以相同的速度向右运动,在运动过程中是否在某个位置使得![]()
![]() 成立?若存在,请你在图中画出此时 PQ 的位置(用线段
成立?若存在,请你在图中画出此时 PQ 的位置(用线段 ![]() 表示),若不存在,请你说明理由(注:画图时,先用铅笔画好,再用钢笔描黑).
表示),若不存在,请你说明理由(注:画图时,先用铅笔画好,再用钢笔描黑).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在反比例函数y=﹣ ![]() 的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=
的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y= ![]() 的图象上运动.若tan∠CAB=2,则k的值为( )
的图象上运动.若tan∠CAB=2,则k的值为( ) 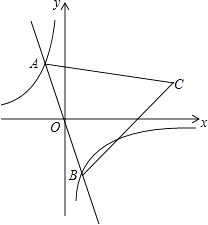
A.2
B.4
C.6
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真观察图形,解答下列问题:
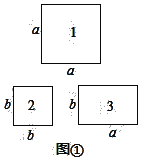
如图①,1号卡片是边长为a的正方形,2号卡片是边长为b的正方形,3号卡片是一个长和宽分别为a,b的长方形.
(1)若选取1号、2号、3号卡片分别为1张、1张、2张,可拼成一个正方形,如图②,能用此图解释的乘法公式是______________;(请用字母a,b表示)
(2)若选取1号、2号、3号卡片分别为1张、2张、3张,可拼成一个长方形(不重叠无缝隙),则能用此图解释的整式乘法运算是____________________;(请画出图形,并用字母a,b表示)
(3)如果图中的a,b(a>b)满足a2+b2=57,ab=12,求a+b的值;
(4)已知(5+2x)2+(3+2x)2=60,求(5+2x)(2x+3)的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间. 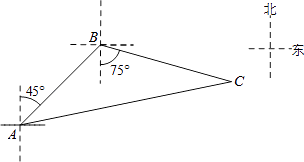
查看答案和解析>>
科目:初中数学 来源: 题型:
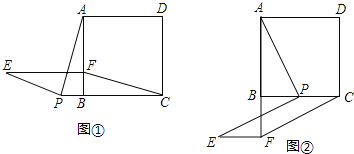
【题目】如图,正方形ABCD中,点P是直线BC上一点,连接PA,将线段PA绕 点P逆时针旋转90°得到线段PE,在直线BA上取点F,使BF=BP,且点F与点E在BC同侧,连接EF、CF.
(1)如图①,当点P在CB延长线上时,求证:四边形PCFE是平行四边形.
(2)如图②,当点P在线段BC上时,四边形PCFE是否还是平行四边形,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列解题过程,然后回答问题:
解方程: ![]()
解:①当![]() ≥0时,原方程可化为:
≥0时,原方程可化为: ![]() ,解得
,解得![]() ;
;
②当![]() <0时,原方程可化为:
<0时,原方程可化为: ![]() ,解得
,解得![]() ;
;
所以原方程的解是![]() 或
或![]()
(1)解方程: ![]()
(2)探究:当![]() 为何值时,方程
为何值时,方程![]() ①无解;②只有一个解;③有两个解。
①无解;②只有一个解;③有两个解。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com