
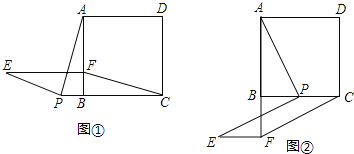
【题目】如图,正方形ABCD中,点P是直线BC上一点,连接PA,将线段PA绕 点P逆时针旋转90°得到线段PE,在直线BA上取点F,使BF=BP,且点F与点E在BC同侧,连接EF、CF.
(1)如图①,当点P在CB延长线上时,求证:四边形PCFE是平行四边形.
(2)如图②,当点P在线段BC上时,四边形PCFE是否还是平行四边形,说明理由.
【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)由正方形的性质可以得出AB=BC,∠ABP=∠ABC=∠90°,可以得出△PBA≌△FBC,由其性质就可以得出结论;
(2)由正方形的性质可以得出AB=BC,∠FBC=∠ABC=∠90°,可以得出△PBA≌△FBC,由其性质就可以得出结论.
试题解析:(1)证明:∵在正方形ABCD中,AB=BC,∠ABC=∠ABP=90,
又∵BF=BP,
∴△BCF≌△BAP(SAS),
∴CF=AP,∠BFC=∠BPA.
又由旋转得:∠EPA=90,PA=PE,
∴PE=CF.∵∠BFC+∠BCF=90
∴∠BPA+∠BCF=90,
∴∠BPA+∠EPA+∠BCF=180,
∴PE∥CF.
∴四边形PCFE为平行四边形.
(2)四边形PCEF是平行四边形.
证明:同(1)得:△BCF≌△BAP,
∴∠BCF=∠BAP,AP=CF.
由旋转得:AP=PE,∠EPA=90,
∴PE=CF.
∴∠BPE+∠BPA=90,
∵在△ABP中,∠ABP=90
∴∠BAP+∠BPA=90,∠BPE=∠BAP,
∴∠BPE=∠BCF,
∴PE∥CF,
∴四边形PCFE为平行四边形.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】绵阳人民商场准备购进甲、乙两种牛奶进行销售,若甲种牛奶的进价比乙种牛奶的进价每件少5元,其用90元购进甲种牛奶的数量与用100元购进乙种牛奶的数量相同.
(1)求甲种牛奶、乙种牛奶的进价分别是多少元?
(2)若该商场购进甲种牛奶的数量是乙种牛奶的3倍少5件,两种牛奶的总数不超过95件,该商场甲种牛奶的销售价格为49元,乙种牛奶的销售价格为每件55元,则购进的甲、乙两种牛奶全部售出后,可使销售的总利润(利润=售价﹣进价)超过371元,请通过计算求出该商场购进甲、乙两种牛奶有哪几种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F. 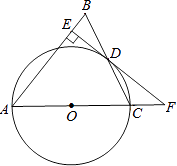
(1)求证:EF是⊙O的切线;
(2)若EB= ![]() ,且sin∠CFD=
,且sin∠CFD= ![]() ,求⊙O的半径与线段AE的长.
,求⊙O的半径与线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在“6·26国际禁毒日”前组织七年级全体学生320人进行了一次“毒品预防知识”竞赛,赛后随机抽取了部分学生成绩进行统计,制作了频数分布表和频数分布直方图.请根据图表中提供的信息,解答下列问题:


(1)表中![]() =___,
=___, ![]() =____,并补全直方图;
=____,并补全直方图;
(2)若用扇形统计图描述此成绩统计分布情况,则分数段80≤![]() <100对应扇形的圆心角度数是___;
<100对应扇形的圆心角度数是___;
(3)请估计该年级分数在60≤![]() <70的学生有多少人?
<70的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在手工制作课上,老师组织七年级(2)班的学生用硬纸制作圆柱形茶叶筒.七年级(2)班共有学生44人,其中男生人数比女生人数少2人,并且每名学生每小时剪筒身50个或剪筒底120个.
(1)七年级(2)班有男生、女生各多少人?
(2)要求一个筒身配两个筒底,为了使每小时剪出的筒身与筒底刚好配套,应该分配多少名学生剪筒身,多少名学生剪筒底?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx+c与x轴交于A(5,0),B(﹣1,0)两点,与y轴交于点C(0, ![]() ).
).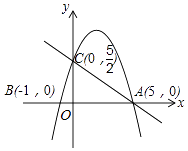
(1)求抛物线的解析式;
(2)在抛物线上是否存在点P,使得△ACP是以点A为直角顶点的直角三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;
(3)点G为抛物线上的一动点,过点G作GE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为点F,连接EF,当线段EF的长度最短时,求出点G的坐标.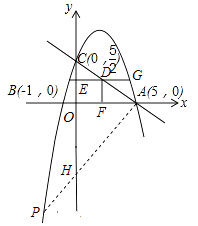
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b(k≠0)和反比例函数y2= ![]() (m≠0)的图象交于点A(﹣1,6),B(a,﹣2).
(m≠0)的图象交于点A(﹣1,6),B(a,﹣2). 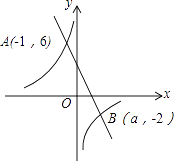
(1)求一次函数与反比例函数的解析式;
(2)根据图象直接写出y1>y2时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”假期,成都某公司组织部分员工分别到甲、乙、丙、丁四地考察,公司按定额购买了前往各地的车票,如图是用来制作完整的车票种类和相应数量的条形统计图,根据统计图回答下列问题:
![]() 若去丙地的车票占全部车票的
若去丙地的车票占全部车票的![]() ,则总票数为______ 张,去丁地的车票有______ 张
,则总票数为______ 张,去丁地的车票有______ 张![]()
![]() 若公司采用随机抽取的方式发车票,小胡先从所有的车票中随机抽取一张
若公司采用随机抽取的方式发车票,小胡先从所有的车票中随机抽取一张![]() 所有车票的形状、大小、质地完全相同、均匀
所有车票的形状、大小、质地完全相同、均匀![]() ,那么员工小胡抽到去甲地的车票的概率是多少?
,那么员工小胡抽到去甲地的车票的概率是多少?
![]() 若有一张车票,小王和小李都想要,他们决定采取掷一枚质地均匀的正方体骰子的方式来确定给谁,其上的数字是3的倍数,则给小王,否则给小李
若有一张车票,小王和小李都想要,他们决定采取掷一枚质地均匀的正方体骰子的方式来确定给谁,其上的数字是3的倍数,则给小王,否则给小李![]() 请问这个规则对双方是否公平?若公平请说明理由;若不公平,请通过计算说明对谁更有利.
请问这个规则对双方是否公平?若公平请说明理由;若不公平,请通过计算说明对谁更有利.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com