
【题目】绵阳人民商场准备购进甲、乙两种牛奶进行销售,若甲种牛奶的进价比乙种牛奶的进价每件少5元,其用90元购进甲种牛奶的数量与用100元购进乙种牛奶的数量相同.
(1)求甲种牛奶、乙种牛奶的进价分别是多少元?
(2)若该商场购进甲种牛奶的数量是乙种牛奶的3倍少5件,两种牛奶的总数不超过95件,该商场甲种牛奶的销售价格为49元,乙种牛奶的销售价格为每件55元,则购进的甲、乙两种牛奶全部售出后,可使销售的总利润(利润=售价﹣进价)超过371元,请通过计算求出该商场购进甲、乙两种牛奶有哪几种方案?
【答案】
(1)解:设乙种牛奶的进价为每件x元,则甲种牛奶的进价为每件(x﹣5)元,
由题意得, ![]() =
= ![]() ,解得x=50.
,解得x=50.
经检验,x=50是原分式方程的解,且符合实际意义
(2)解:设购进乙种牛奶y件,则购进甲种牛奶(3y﹣5)件,
由题意得 ![]() ,解得23<y≤25.
,解得23<y≤25.
∵y为整数,
∴y=24或25,
∴共有两种方案:
方案一:购进甲种牛奶67件,乙种牛奶24件;
方案二:购进甲种牛奶70件,乙种牛奶25件
【解析】(1)设乙种牛奶的进价为每件x元,则甲种牛奶的进价为每件(x﹣5)元,由题意列出关于x的方程,求出x的值即可;(2)设购进乙种牛奶y件,则购进甲种牛奶(3y﹣5)件,根据题意列出关于y的不等式组,求出y的整数解即可得出结论.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】体育课上,全班男同学进行了100米测验,达标成绩为15秒,如表是某小组8名男生的成绩记录,其中“![]() “表示成绩大于15秒.
“表示成绩大于15秒.
|
|
|
|
|
|
|
|
问:![]() 这个小组男生最优秀的成绩是多少秒?最差的成绩是多少秒?
这个小组男生最优秀的成绩是多少秒?最差的成绩是多少秒?
![]() 这个小组男生的达标率为多少?
这个小组男生的达标率为多少?![]() 达标率
达标率![]()
![]() 这个小组男生的平均成绩是多少秒?
这个小组男生的平均成绩是多少秒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算:
(1)78-23÷70=70÷70=1;
(2)12-7×(-4)+8÷(-2)=12+28-4=36;
(3)12÷(2×3)=12÷2×3=6×3=18;
(4)32×3.14+3×(-9.42)=3×9.42+3×(-9.42)=0.
其中错误的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,AB=AC,AB 的垂直平分线交 AB 于点 D,交 CA 的延长线于点 E,∠EBC=42°,则 ∠BAC=( )

A. 159° B. 154° C. 152° D. 138°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P与点 Q 都在y轴上,且关于x轴对称.
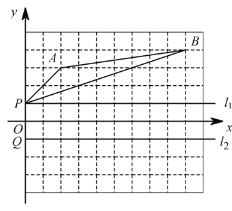
(1)请画出△ABP 关于x轴的对称图形 ![]() (其中点 A 的对称点用
(其中点 A 的对称点用 ![]() 表示,点 的对称点用
表示,点 的对称点用 ![]() 表示);
表示);
(2)点P ,Q 同时都从y轴上的位置出发,分别沿l1,l2方向,以相同的速度向右运动,在运动过程中是否在某个位置使得![]()
![]() 成立?若存在,请你在图中画出此时 PQ 的位置(用线段
成立?若存在,请你在图中画出此时 PQ 的位置(用线段 ![]() 表示),若不存在,请你说明理由(注:画图时,先用铅笔画好,再用钢笔描黑).
表示),若不存在,请你说明理由(注:画图时,先用铅笔画好,再用钢笔描黑).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在反比例函数y=﹣ ![]() 的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=
的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y= ![]() 的图象上运动.若tan∠CAB=2,则k的值为( )
的图象上运动.若tan∠CAB=2,则k的值为( ) 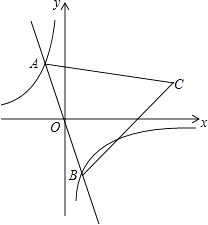
A.2
B.4
C.6
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
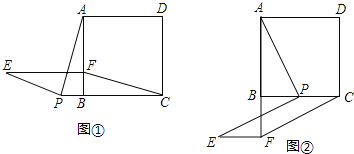
【题目】如图,正方形ABCD中,点P是直线BC上一点,连接PA,将线段PA绕 点P逆时针旋转90°得到线段PE,在直线BA上取点F,使BF=BP,且点F与点E在BC同侧,连接EF、CF.
(1)如图①,当点P在CB延长线上时,求证:四边形PCFE是平行四边形.
(2)如图②,当点P在线段BC上时,四边形PCFE是否还是平行四边形,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com