
【题目】体育课上,全班男同学进行了100米测验,达标成绩为15秒,如表是某小组8名男生的成绩记录,其中“![]() “表示成绩大于15秒.
“表示成绩大于15秒.
|
|
|
|
|
|
|
|
问:![]() 这个小组男生最优秀的成绩是多少秒?最差的成绩是多少秒?
这个小组男生最优秀的成绩是多少秒?最差的成绩是多少秒?
![]() 这个小组男生的达标率为多少?
这个小组男生的达标率为多少?![]() 达标率
达标率![]()
![]() 这个小组男生的平均成绩是多少秒?
这个小组男生的平均成绩是多少秒?
 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AD=BC=6,AB=CD=4.点P从点A出发,以每秒1个单位的速度沿A→B→C→D→A的方向运动,回到点A停止运动.设运动时间为t秒.
(1)当t= 时,点P到达点C;当t= 时,点P回到点A;
(2)△ABP面积取最大值时t的取值范围;(3)当△ABP的面积为3时,求t的值;
(4)若点P出发时,点Q从点A出发,以每秒2个单位的速度沿A→D→C→B→A的方向运动,回到点A停止运动.请问:P 、Q何时在长方形ABCD的边上相距1个单位长度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解题过程:
计算:(-5)÷![]() ×20.
×20.
解:原式=(-5)÷![]() ×20 (第一步)
×20 (第一步)
=(-5)÷(-1) (第二步)
=-5. (第三步)
(1)上述解题过程中有两处错误:
第一处是第________步,错误的原因是__________________________;
第二处是第________步,错误的原因是_______________________.
(2)把正确的解题过程写出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司仓库本周内货物进出的吨数记录如下![]() “
“![]() ”表示进库,“
”表示进库,“![]() ”表示出库
”表示出库![]() ;
;
日期 | 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
吨数 |
|
|
|
|
|
|
|
![]() 这一周,仓库内货物的总吨数是______了
这一周,仓库内货物的总吨数是______了![]() 填“增多”或“减少”
填“增多”或“减少”![]() ;
;
若周六结束时仓库内还有货物360吨,则周日开始时仓库内有货物多少吨?
![]() 如果该仓库货物进出的装卸费都是每吨5元,那么这一周内共需付多少元的装卸费?
如果该仓库货物进出的装卸费都是每吨5元,那么这一周内共需付多少元的装卸费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在矩形ABCD中,AB=10 cm,BC=8 cm.点P从点A出发,沿A→B→C→D的路线运动,到点D停止;点Q从点D出发,沿D→C→B→A的路线运动,到点A停止.若点P、点Q同时出发,点P的速度为每秒1 cm,点Q的速度为每秒2 cm,a秒时,点P、点Q同时改变速度,点P的速度变为每秒b cm,点Q的速度变为每秒d cm.图②是点P出发x秒后△APD的面积S1(cm2)与时间x(秒)的函数关系图象;图③是点Q出发x秒后△AQD的面积S2(cm2)与时间x(秒)的函数关系图象.

(1)参照图②,求a、 b及图②中c的值;
(2)求d的值;
(3)设点P离开点A的路程为y1(cm),点Q到点A还需要走的路程为y2(cm),请分别写出改变速度后,y1、y2与出发后的运动时间x(秒)的函数关系式,并求出点P、点Q相遇时x的值;
(4)当点Q出发__ __秒时,点Q的运动路程为25 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒. 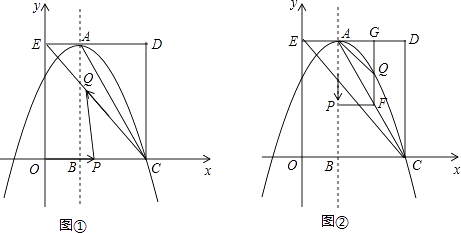
(1)填空:点A坐标为;抛物线的解析式为 .
(2)在图①中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图②中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元。厂方在开展促销活动期间,向客户提供两种优惠方案:
①买一套西装送一条领带;②西装和领带都按定价的90%付款。现某客户要到该服装厂购买西装20套,领带x条(![]() ):
):
(1)若该客户按方案①购买,需付款______________元(用含x的代数式表示);若该客户按方案②购买,需付款________________元(用含x的代数式表示);
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
(3)当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绵阳人民商场准备购进甲、乙两种牛奶进行销售,若甲种牛奶的进价比乙种牛奶的进价每件少5元,其用90元购进甲种牛奶的数量与用100元购进乙种牛奶的数量相同.
(1)求甲种牛奶、乙种牛奶的进价分别是多少元?
(2)若该商场购进甲种牛奶的数量是乙种牛奶的3倍少5件,两种牛奶的总数不超过95件,该商场甲种牛奶的销售价格为49元,乙种牛奶的销售价格为每件55元,则购进的甲、乙两种牛奶全部售出后,可使销售的总利润(利润=售价﹣进价)超过371元,请通过计算求出该商场购进甲、乙两种牛奶有哪几种方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com