
【题目】某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元。厂方在开展促销活动期间,向客户提供两种优惠方案:
①买一套西装送一条领带;②西装和领带都按定价的90%付款。现某客户要到该服装厂购买西装20套,领带x条(![]() ):
):
(1)若该客户按方案①购买,需付款______________元(用含x的代数式表示);若该客户按方案②购买,需付款________________元(用含x的代数式表示);
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
(3)当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法。
【答案】(1)3200+40x;3600+36x(2)方案一购买较为合算(3)可以。
【解析】
试题分析:(1)若该客户按方案①购买,20×200+40(x-20)=3200+40x
若该客户按方案②购买:(20×200+40x)90%=3600+36x
(2)解:当x=40时,
方案一:3200+40×30=3200+1200=4400(元)
方案二: 3600+36×30=3600+1080=4680(元)
4200元<4680元
答:此时方案一购买较为合算。
(3)可以。
用方案一买20套西装和20条领带,再用方案二买10条领带。总价钱为:
20×200+40×10×90%=4000+360=4360(元)
∵4360<4400,∴可以。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F. 
(1)证明:∠BAE=∠FEC;
(2)证明:△AGE≌△ECF;
(3)求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,全班男同学进行了100米测验,达标成绩为15秒,如表是某小组8名男生的成绩记录,其中“![]() “表示成绩大于15秒.
“表示成绩大于15秒.
|
|
|
|
|
|
|
|
问:![]() 这个小组男生最优秀的成绩是多少秒?最差的成绩是多少秒?
这个小组男生最优秀的成绩是多少秒?最差的成绩是多少秒?
![]() 这个小组男生的达标率为多少?
这个小组男生的达标率为多少?![]() 达标率
达标率![]()
![]() 这个小组男生的平均成绩是多少秒?
这个小组男生的平均成绩是多少秒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(﹣4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s). 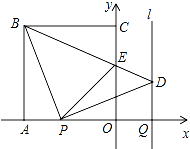
(1)∠PBD的度数为 , 点D的坐标为(用t表示);
(2)当t为何值时,△PBE为等腰三角形?
(3)探索△POE周长是否随时间t的变化而变化?若变化,说明理由;若不变,试求这个定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分解因式2a(b+c)-3(b+c)的结果是______.
【答案】(b+c)(2a-3)
【解析】解析:2a(b+c)-3(b+c)=(b+c)(2a-3).
点睛:因式分解的方法:(1)提取公因式法.ma+mb+mc=m(a+b+c).
(2)公式法:完全平方公式,平方差公式.
(3)十字相乘法.
因式分解的时候,要注意整体换元法的灵活应用,训练将一个式子看做一个整体,利用上述方法因式分解的能力.
【题型】填空题
【结束】
17
【题目】在我们所学的课本中,多项式与多项式相乘可以用几何图形的面积来表示.例如,(2a+b)(a+b)=2a2+3ab+b2就可以用图(1)来表示.请你根据此方法写出图(2)中图形的面积所表示的代数恒等式:____________.
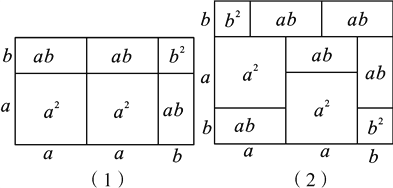
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在反比例函数y=﹣ ![]() 的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=
的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y= ![]() 的图象上运动.若tan∠CAB=2,则k的值为( )
的图象上运动.若tan∠CAB=2,则k的值为( ) 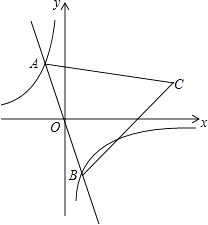
A.2
B.4
C.6
D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com