
【题目】如图,长方形ABCD中,AD=BC=6,AB=CD=4.点P从点A出发,以每秒1个单位的速度沿A→B→C→D→A的方向运动,回到点A停止运动.设运动时间为t秒.
(1)当t= 时,点P到达点C;当t= 时,点P回到点A;
(2)△ABP面积取最大值时t的取值范围;(3)当△ABP的面积为3时,求t的值;
(4)若点P出发时,点Q从点A出发,以每秒2个单位的速度沿A→D→C→B→A的方向运动,回到点A停止运动.请问:P 、Q何时在长方形ABCD的边上相距1个单位长度?

【答案】(1)当t=10,点p到点C,当t=20,点p到点A;(2)10≤t≤14;(3)t=5.5或t=18.5; (4)t=![]() 或 t=7.
或 t=7.
【解析】
(1)根据长方形ABCD的边长和点P的运动速度进行计算即可;
(2)由图可知,当点P在边CD上运动时,△ABP的面积最大,由此根据已知条件计算出点P在边CD上运动所对应的时间范围即可;
(3)如图1和图2,分点P在BC上和AD上两种情况结合已知条件解答即可;
(4)由题意可知,点P、Q在长方形ABCD上从A点出发,作相向运动,因此存在以下两种情况: ①点P、Q相遇前相距1个单位长度,如下图3所示;②点P、Q相遇后相距1个单位长度,如下图4所示;结合已知条件分这两种情况解答即可.
(1)∵AD=BC=6,AB=CD=4,
∴AB+BC=10,AB+BC+CD+DA=20,
又∵点P的移动速度为每秒1个单位长度,
∴点P由A到C所需时间为:10÷1=10(秒),
点P由A出发回到A所需时间为:20÷1=20(秒);
(2)由图可知,当点P在边CD上运动时,△ABP的面积最大,
∵AB+BC+CD=14,
∴点P移动到点D的时间为:14÷1=14(秒),
又∵点P移动到点C的时间为10秒,
∴当△ABP的面积最大时,![]() ;
;
(3)①如图1,当点P在边BC上时,由已知可得:AB=4,PB=(t-4),由题意可得:
S△ABP=![]() ,解得:
,解得:![]() ;
;
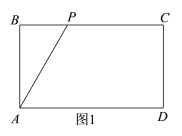
②如图2,当点P在边AD上时,由已知可得:AB=4,AP=(20-t),由题意可得:S△ABP=![]() ,解得:
,解得:![]() ,
,
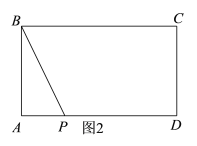
综上所述,当t=5.5或t=18.5时,△ABP的面积为3.
(4)①如图3,当点P、Q相遇前相距1个单位长度时,
由题意可得:![]() ,解得:
,解得:![]() ;
;

②如图4,当点P、Q在相遇后相距1个单位长度时,由题意可得:
![]() ,解得:
,解得:![]() ,
,

综上所述,当![]() 或
或![]() 时,点P、Q在长方形ABCD的边上相距1个单位长度.
时,点P、Q在长方形ABCD的边上相距1个单位长度.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知DE∥BC,BE平分∠ABC,∠C=65°,∠ABC=50°.
(1)求∠BED的度数;
(2)判断BE与AC的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若m2-2mn+2n2-8n+16=0,求m、n的值.
解:∵m2-2mn+2n2-8n+16=0,
∴(m2-2m n+n2)+( )=0,
即( )2+( )2=0.根据非负数的性质,
∴m=n=
完善上述解答过程,然后解答下面的问题:
设等腰三角形ABC的三边长a、b、c,且满足a2+b2-4a-6b+13=0,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD∥EF,∠1=75,∠2=45,点 G为∠BED 内一点,且 EG把∠BED分成 1 ∶ 2 两部分,则∠GEF 的度数为 ___.
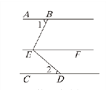
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点 B(m,n) 在第一象限,m,n 均为整数,且满足n =![]() .
.
(1) 求点 B 的坐标;
(2) 将线段 OB 向下平移 a 个单位后得到线段 O′B′,过点 B′作 B′C⊥y 轴于点 C,若 3CO=2CO′,求a 的值;
(3) 过点 B 作与 y 轴平行的直线 BM,点 D 在 x 轴上,点 E 在 BM 上,点 D 从 O 点出发以每秒钟 3个单位长度的速度沿 x 轴向右运动,同时点 E 从 B 点出发以每秒钟 2 个单位长度的速度沿BM 向下运动,在点 D,E 运动的过程中,若直线 OE,BD 相交于点 G,且 5≤S△OGB≤10,则点G 的横坐标 xG的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F. 
(1)证明:∠BAE=∠FEC;
(2)证明:△AGE≌△ECF;
(3)求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,全班男同学进行了100米测验,达标成绩为15秒,如表是某小组8名男生的成绩记录,其中“![]() “表示成绩大于15秒.
“表示成绩大于15秒.
|
|
|
|
|
|
|
|
问:![]() 这个小组男生最优秀的成绩是多少秒?最差的成绩是多少秒?
这个小组男生最优秀的成绩是多少秒?最差的成绩是多少秒?
![]() 这个小组男生的达标率为多少?
这个小组男生的达标率为多少?![]() 达标率
达标率![]()
![]() 这个小组男生的平均成绩是多少秒?
这个小组男生的平均成绩是多少秒?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com