
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO,已知BD=![]() .
.
(1)求正方形ABCD的边长;
(2)求OE的长;
(3)①求证:CN=AF;
②直接写出四边形AFBO的面积.

【答案】(1)2;(2)![]() ;(3)①证明见解析,②
;(3)①证明见解析,②![]()
【解析】试题分析:(1)根据正方形的性质以及勾股定理即可求得;(2)根据等腰三角形三线合一的性质证得点E是AF中点,依据三角形中位线OE=![]() CF=
CF=![]() ;(3) ①通过证明△NCB≌△FAB可证得CN=AF; ②依据△AFC的面积-△BOC的面积.
;(3) ①通过证明△NCB≌△FAB可证得CN=AF; ②依据△AFC的面积-△BOC的面积.
试题解析:
(1)∵四边形ABCD是正方形,
∴AB=CD=BC,∠BCD=∠ABC=90°,
∴2BC2=BD2,∵BD=![]() ,∴AB= BC =2,
,∴AB= BC =2,
∴正方形ABCD的边长为2;
(2)∵CF=CA,AF是∠ACF的平分线,
∴CE⊥AF,∴∠AEC=∠CEF=90°,E为AF的中点,
∵正方形ABCD,∴O为AC的中点,AC=BD=![]() ,
,
∴OE=![]() CF=
CF=![]() BD=
BD=![]() ,
,
(3)①证明:∵∠ABC=∠ABF=∠CEF=90°,AB=BC,
∴∠ECB+∠F=∠FAB+∠F=90°,∴∠ECB=∠FAB,
∴△NCB≌△FAB,
∴CN=AF.
②![]() .
.
点睛:本题综合考查了菱形、矩形、正方形的有关性质及判定,其中还串联到等腰三角形和勾股定理等知识,充分体现出几何知识的整体性和推理的严密性.在解答有关特殊四边形的性质或判定问题时,既要依托数,也要依托形,这是解答几何问题的最基本的思想方法.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为( ) 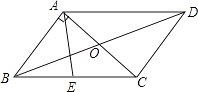
A.3cm
B.4cm
C.5cm
D.8cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并回答问题: 材料1:如果一个三角形的三边长分别为a,b,c,记 ![]() ,那么三角形的面积为
,那么三角形的面积为 ![]() . ①
. ①
古希腊几何学家海伦(Heron,约公元50年),在数学史上以解决几何测量问题而闻名.他在《度量》一书中,给出了公式①和它的证明,这一公式称海伦公式.
我国南宋数学家秦九韶(约1202﹣﹣约1261),曾提出利用三角形的三边求面积的秦九韶公式: ![]() . ②
. ②
下面我们对公式②进行变形: ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
这说明海伦公式与秦九韶公式实质上是同一公式,所以我们也称①为海伦﹣﹣秦九韶公式.
问题:如图,在△ABC中,AB=13,BC=12,AC=7,⊙O内切于△ABC,切点分别是D、E、F.
(1)求△ABC的面积;
(2)求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】云南地区地震发生后,市政府筹集了必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)

(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节省运费,市政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能求出这三种车型分别有多少辆吗?此时的运费又是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,∠BOM=90°,∠DON=90°.
(1)若∠COM=∠AOC,求∠AOD的度数;
(2)若∠COM=![]() ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() 与一次函数y=ax+b的图象交于点A(2,2)、B(
与一次函数y=ax+b的图象交于点A(2,2)、B( ![]() ,n).
,n). 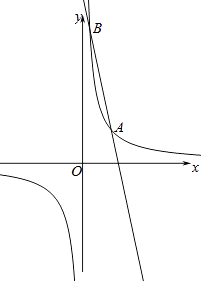
(1)求这两个函数解析式;
(2)将一次函数y=ax+b的图象沿y轴向下平移m个单位,使平移后的图象与反比例函数y= ![]() 的图象有且只有一个交点,求m的值.
的图象有且只有一个交点,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,O为直线AB上一点,过点O作射线OC,使∠BOC=110°.将一三角尺的直角顶点放在点O处(∠OMN=30°),一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图①中的三角尺绕点O逆时针旋转至图②,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠BON的度数;
(2)将图①中的三角尺绕点O以每秒5°的速度按逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为________(直接写出结果);
(3)将图①中的三角尺绕点O顺时针旋转至图③,使ON在∠AOC的内部,请探究∠AOM与∠NOC的数量关系,并说明理由.
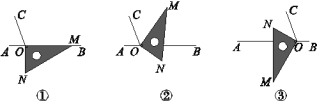
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数-5,1,-3,5,-2中任取三个数相乘,其中最大的积是a,最小的积是b.
(1)求a,b的值;
(2)若|x+a|+|y-b|=0,求(x+y)÷(x-y)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某城市市民广场一入口处有五级高度相等的小台阶.已知台阶总高1.5米,为了安全,现要做一个不锈钢扶手AB及两根与FG垂直且长为1米的不锈钢架杆AD和BC(杆子的底端分别为D、C),且∠DAB=66.5°.(参考数据:cos66.5°≈0.40,sin66.5°≈0.92) 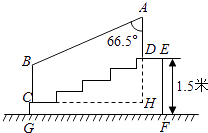
(1)求点D与点C的高度差DH;
(2)求所有不锈钢材料的总长度(即AD+AB+BC的长,结果精确到0.1米)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com