练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，平行四边形ABCD的周长是26cm，对角线AC与BD交于点O，AC⊥AB，E是BC中点，△AOD的周长比△AOB的周长多3cm，则AE的长度为（ ）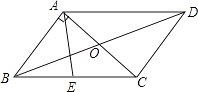
    A.3cm
    B.4cm
    C.5cm
    D.8cm

    【答案】B
    【解析】解：∵ABCD的周长为26cm， ∴AB+AD=13cm，OB=OD，
    ∵△AOD的周长比△AOB的周长多3cm，
    ∴（OA+OD+AD）﹣（OA+OB+AB）=AD﹣AB=3cm，
    ∴AB=5cm，AD=8cm．
    ∴BC=AD=8cm．
    ∵AC⊥AB，E是BC中点，
    ∴AE= BC=4cm；
    故选：B．
    由ABCD的周长为26cm，对角线AC、BD相交于点O，若△AOD的周长比△AOB的周长多3cm，可得AB+AD=13cm，AD﹣AB=3cm，求出AB和AD的长，得出BC的长，再由直角三角形斜边上的中线性质即可求得答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下列各式计算正确的是( )

    A. 7－2×(－)＝5×(－)＝－1 B. －3÷7×＝－3÷1＝－3

    C. －32－(－3)2＝－9－9＝－18 D. 3×23－2×9＝3×6－18＝0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形OABC的边OA，OC在坐标轴上，点B的坐标为（﹣4，4）．点P从点A出发，以每秒1个单位长度的速度沿x轴向点O运动；点Q从点O同时出发，以相同的速度沿x轴的正方向运动，规定点P到达点O时，点Q也停止运动．连接BP，过P点作BP的垂线，与过点Q平行于y轴的直线l相交于点D．BD与y轴交于点E，连接PE．设点P运动的时间为t（s）．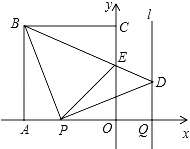
    （1）∠PBD的度数为 ， 点D的坐标为（用t表示）；
    （2）当t为何值时，△PBE为等腰三角形？
    （3）探索△POE周长是否随时间t的变化而变化？若变化，说明理由；若不变，试求这个定值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，数轴上点A表示数x，点B表示－2，点C表示数2x＋8.

    (1)若将数轴沿点B对折，点A与点C恰好重合，则点A和点C分别表示什么数？

    (2)若BC＝4AB，则点A和点C分别表示什么数？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】分解因式2a（b+c）-3（b+c）的结果是______.

    【答案】（b+c）（2a-3）

    【解析】解析：2a（b+c）-3（b+c）=（b+c）（2a-3）.

    点睛：因式分解的方法：（1）提取公因式法.ma+mb+mc=m(a+b+c).

    （2）公式法:完全平方公式，平方差公式.

    （3）十字相乘法.

    因式分解的时候，要注意整体换元法的灵活应用，训练将一个式子看做一个整体,利用上述方法因式分解的能力.

    【题型】填空题
    【结束】
    17

    【题目】在我们所学的课本中，多项式与多项式相乘可以用几何图形的面积来表示.例如，（2a+b）（a+b）=2a2+3ab+b2就可以用图（1）来表示.请你根据此方法写出图（2）中图形的面积所表示的代数恒等式：____________.

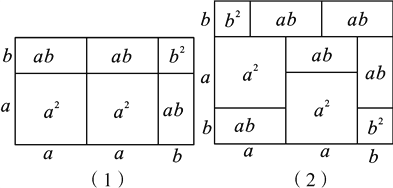
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中AB=AC=4，∠C=72°，D是AB中点，点E在AC上，DE⊥AB，则cosA的值为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点E，点F分别在菱形ABCD的边AB，AD上，且AE=DF，BF交DE于点G，延长BF交CD的延长线于H，若 =2，则 的值为（ ）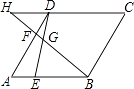
    A. ??
    B. ??
    C. ??
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB为⊙O直径，C为⊙O上一点，点D是 的中点，DE⊥AC于E，DF⊥AB于F．
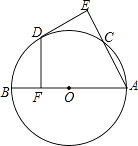
    （1）判断DE与⊙O的位置关系，并证明你的结论；
    （2）若OF=4，求AC的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的对角线AC，BD相交于点O，延长CB至点F，使CF=CA，连接AF，∠ACF的平分线分别交AF，AB，BD于点E，N，M，连接EO，已知BD=．

    （1）求正方形ABCD的边长；

    （2）求OE的长；

    （3）①求证：CN＝AF；

    ②直接写出四边形AFBO的面积．

    查看答案和解析>>

    同步练习册答案