
【题目】如图,点E,点F分别在菱形ABCD的边AB,AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于H,若 ![]() =2,则
=2,则 ![]() 的值为( )
的值为( ) 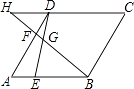
A.![]() ??
??
B.![]() ??
??
C.![]() ??
??
D.![]()
科目:初中数学 来源: 题型:
【题目】阅读材料:
对于线段的垂直平分线我们有如下结论:到线段两个端点距离相等的点在线段的垂直平分线上.即如图①,若PA=PB,则点P在线段AB的垂直平分线上.

请根据阅读材料,解决下列问题:
如图②,直线CD是等边△ABC的对称轴,点D在AB上,点E是线段CD上的一动点(点E不与点C、D重合),连结AE、BE,△ABE经顺时针旋转后与△BCF重合.
(1)旋转中心是点 ,旋转了 (度);
(2)当点E从点D向点C移动时,连结AF,设AF与CD交于点P,在图②中将图形补全,并探究∠APC的大小是否保持不变?若不变,请求出∠APC的度数;若改变,请说出变化情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列等式成立的是( )
A. (-a-b)2+(a-b)2=-4ab B. (-a-b)2+(a-b)2=a2+b2
C. (-a-b)(a-b)=(a-b)2 D. (-a-b)(a-b)=b2-a2
【答案】D
【解析】解析:∵(-a-b)2+(a-b)2=(a+b)2+(a-b)2=(a2+2ab+b2)+(a2-2ab+b2)=2a2+2b2,
∴选项A与选项B错误;
∵(-a-b)(a-b)=-(a+b)(a-b)=-(a2-b2)=b2-a2,∴选项C错误,选项D正确.
故选D.
【题型】单选题
【结束】
8
【题目】若x=1,y=![]() ,则x2+4xy+4y2的值是( )
,则x2+4xy+4y2的值是( )
A. 2 B. 4 C. 32 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为( ) 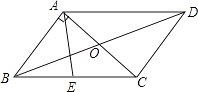
A.3cm
B.4cm
C.5cm
D.8cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE是AB的延长线,指出下面各组中的两个角是由哪两条直线被哪一条直线所截形成的?它们是什么角?
(1)∠A和∠D;
(2)∠A和∠CBA;
(3)∠C和∠CBE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°,且m°的角与n°的角互余.
(1)①若m=50,则射线OC的方向是________;
②图中与∠BOE互余的角有__________,与∠BOE互补的角有__________.
(2)若射线OA是∠BON的平分线,则∠BOS与∠AOC是否存在确定的数量关系?如果存在,请写出你的结论以及计算过程;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并回答问题: 材料1:如果一个三角形的三边长分别为a,b,c,记 ![]() ,那么三角形的面积为
,那么三角形的面积为 ![]() . ①
. ①
古希腊几何学家海伦(Heron,约公元50年),在数学史上以解决几何测量问题而闻名.他在《度量》一书中,给出了公式①和它的证明,这一公式称海伦公式.
我国南宋数学家秦九韶(约1202﹣﹣约1261),曾提出利用三角形的三边求面积的秦九韶公式: ![]() . ②
. ②
下面我们对公式②进行变形: ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
这说明海伦公式与秦九韶公式实质上是同一公式,所以我们也称①为海伦﹣﹣秦九韶公式.
问题:如图,在△ABC中,AB=13,BC=12,AC=7,⊙O内切于△ABC,切点分别是D、E、F.
(1)求△ABC的面积;
(2)求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
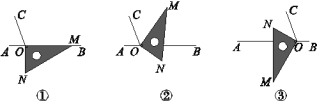
【题目】如图①,O为直线AB上一点,过点O作射线OC,使∠BOC=110°.将一三角尺的直角顶点放在点O处(∠OMN=30°),一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图①中的三角尺绕点O逆时针旋转至图②,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠BON的度数;
(2)将图①中的三角尺绕点O以每秒5°的速度按逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为________(直接写出结果);
(3)将图①中的三角尺绕点O顺时针旋转至图③,使ON在∠AOC的内部,请探究∠AOM与∠NOC的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com