
【题目】如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°,且m°的角与n°的角互余.
(1)①若m=50,则射线OC的方向是________;
②图中与∠BOE互余的角有__________,与∠BOE互补的角有__________.
(2)若射线OA是∠BON的平分线,则∠BOS与∠AOC是否存在确定的数量关系?如果存在,请写出你的结论以及计算过程;如果不存在,请说明理由.

【答案】 (1)①北偏东40° ; ② ∠BOS,∠COE ;∠BOW,∠SOC;(2)∠AOC=![]() ∠BOS.
∠BOS.
【解析】
(1)①由m=50,m+n=90°可求n的值,从而得到结论;
②余角和补角的定义,可得答案;
(2)根据OA是∠BON的角平线,可得∠NOA与∠NOB的关系,根据两角互补,可得∠BON与∠SOB的关系,再根据角平分线,可得∠NOA与∠NOB的关系,根据两角互余,可得∠NOC与∠SOB的关系,根据角的和差,可得答案.
(1)①若m=50,m+n=90°,n=40°,
则射线OC的方向是北偏东40°;
②∠BOS+∠BOE=90°,图中与∠BOE互余的角有∠BOS,
由m°的角与n°的角互余,∠BOE+COE=90°, 得图中与∠BOE互余的角有∠COE,
∠BOE+BOW=180°,∠BOE互补的角有∠BOW.
∵∠NOC+∠COE=90°,∠EOC+∠BOE=90°,∴∠BOE=∠NOC.
∵∠NOC+∠SOC=180°,∴∠BOE互补的角有∠SOC.
故答案为:北偏东40°;∠BOS,∠COE;∠BOW,∠SOC.
(2)∠AOC=![]() .
.
∵射线OA是∠BON的角平分线,∴∠NOA=![]() ∠NOB,
∠NOB,
∵∠SOB+∠BON=180°,
∠BON=180°﹣∠SOB,
∠NOA=![]() ∠BON=90
∠BON=90![]() ,
,
∵∠NOC+∠SOB=90°,∠NOC=90°﹣∠SOB,
∠AOC=N0A﹣∠NOC=90°﹣![]() ﹣(90°﹣∠SOB)
﹣(90°﹣∠SOB)
∴∠AOC=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,动点P从点A开始沿A→B→C→D 的路径匀速前进到D为止.在这个过程中,△APD的面积S随时间t的变化关系用图象表示正确的是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分解因式2a(b+c)-3(b+c)的结果是______.
【答案】(b+c)(2a-3)
【解析】解析:2a(b+c)-3(b+c)=(b+c)(2a-3).
点睛:因式分解的方法:(1)提取公因式法.ma+mb+mc=m(a+b+c).
(2)公式法:完全平方公式,平方差公式.
(3)十字相乘法.
因式分解的时候,要注意整体换元法的灵活应用,训练将一个式子看做一个整体,利用上述方法因式分解的能力.
【题型】填空题
【结束】
17
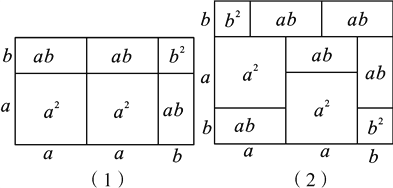
【题目】在我们所学的课本中,多项式与多项式相乘可以用几何图形的面积来表示.例如,(2a+b)(a+b)=2a2+3ab+b2就可以用图(1)来表示.请你根据此方法写出图(2)中图形的面积所表示的代数恒等式:____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E,点F分别在菱形ABCD的边AB,AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于H,若 ![]() =2,则
=2,则 ![]() 的值为( )
的值为( ) 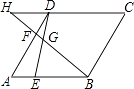
A.![]() ??
??
B.![]() ??
??
C.![]() ??
??
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,C为⊙O上一点,点D是 ![]() 的中点,DE⊥AC于E,DF⊥AB于F.
的中点,DE⊥AC于E,DF⊥AB于F. 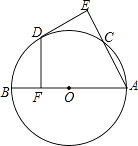
(1)判断DE与⊙O的位置关系,并证明你的结论;
(2)若OF=4,求AC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,AB=AC,AB 的垂直平分线交 AB 于点 D,交 CA 的延长线于点 E,∠EBC=42°,则 ∠BAC=( )

A. 159° B. 154° C. 152° D. 138°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有两枚质地均匀的正方体骰子,每枚骰子的六个面上都分别标有数字1、2、3、4、5、6.同时投掷这两枚骰子,以朝上一面所标的数字为掷得的结果,那么所得结果之和为9的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( ) 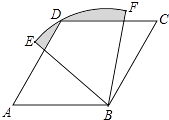
A.![]() ﹣
﹣ ![]() ??
??
B.![]() ﹣
﹣ ![]() ??
??
C.π﹣ ![]() ??
??
D.π﹣ ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com