
 在平面直角坐标系xOy中,抛物线y=mx2-2mx+2(m≠0)与y轴交于点A,其对称轴与x轴交于点B.
在平面直角坐标系xOy中,抛物线y=mx2-2mx+2(m≠0)与y轴交于点A,其对称轴与x轴交于点B.分析 (1)求出x=0时y的值与y=0时x的值即可得答案;
(2)分m>0和m<0两种情况,结合函数图象可得.
解答 解:(1)由题意,当x=0时,y=2.
∴A(0,2).
∵y=mx2-2mx+2=m(x-1)2+2-m,
∴对称轴为直线x=1.
∴B(1,0).
(2)由题意,C(-1,0),D(3,0).
①当m>0时,
结合函数图象可知,满足题意的抛物线的顶点须在x轴下方,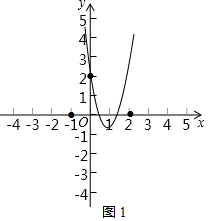
即2-m<0.
∴m>2.
②当m<0时,
过C(-1,0)的抛物线的顶点为E(1,$\frac{8}{3}$).
结合函数图象可知,满足条件的抛物线的顶点须在点E上方或与点E重合,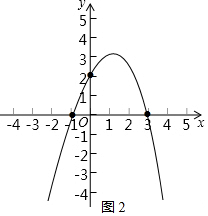
即2-m≥$\frac{8}{3}$.
∴m≤$-\frac{2}{3}$.
综上所述,m的取值范围为m>2或m≤$-\frac{2}{3}$.
点评 本题主要考查抛物线与x轴的交点,熟练掌握二次函数的图象与性质是解题的关键.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:解答题
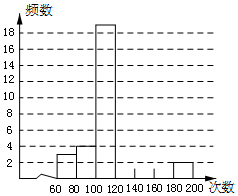 校学生会体育干部想了解七年级学生60秒跳绳的情况,从七年级随机抽取了50名同学的成绩,统计如下:
校学生会体育干部想了解七年级学生60秒跳绳的情况,从七年级随机抽取了50名同学的成绩,统计如下:| 次数分组 | 频数 |
| 60≤x<80 | 3 |
| 80≤x<100 | 4 |
| 100≤x<120 | 19 |
| 120≤x<140 | 10 |
| 140≤x<160 | 8 |
| 160≤x<180 | 4 |
| 180≤x<200 | 2 |
| 合计 | 50 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查市场上老酸奶的质量情况 | |
| B. | 调查某品牌圆珠笔的使用寿命 | |
| C. | 调查乘坐飞机的旅客是否携带了违禁品 | |
| D. | 调查某市初中生的睡眠情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
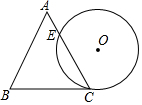 如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则弧CE的长为( )
如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则弧CE的长为( )| A. | 4cm | B. | 3cm | C. | $\frac{2\sqrt{3}π}{3}$cm | D. | $\frac{\sqrt{3}π}{3}$cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com