
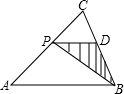
 BC于D,设AP=x.
BC于D,设AP=x.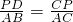 ,
,
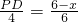 ,PD=
,PD= (6-x),
(6-x), x
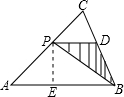
x •PD•PE
•PD•PE ×
× (6-x)×
(6-x)× x
x x2+x(0<x<6);
x2+x(0<x<6); <0,
<0,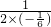 =3,即P为AC中点时,△BPD面积最大,此时PD的长为2.
=3,即P为AC中点时,△BPD面积最大,此时PD的长为2. •PD•PE.分别用含x的式子表示PD、PE.在△APE中易表示PE;利用△CPD∽△CAB表示PD.
•PD•PE.分别用含x的式子表示PD、PE.在△APE中易表示PE;利用△CPD∽△CAB表示PD.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com