
ij��װ��˾����һ�ֳɱ�Ϊÿ��50Ԫ��T�������涨����ʱ�����۵��۲����ڳɱ��ۣ��ֲ�����ÿ��70Ԫ�������������� �����������۵���
�����������۵���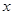 ��Ԫ���Ĺ�ϵ���Խ��ƵĿ���һ�κ�������ͼ����
��Ԫ���Ĺ�ϵ���Խ��ƵĿ���һ�κ�������ͼ����
��1���� ��
��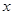 ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2���蹫˾��õ������������� �����۶�
�����۶� �ܳɱ���Ϊ
�ܳɱ���Ϊ Ԫ����
Ԫ���� ��
��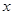 ֮��ĺ�����ϵʽ����д���Ա���
֮��ĺ�����ϵʽ����д���Ա���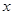 ��ȡֵ��Χ�����������жϣ���
��ȡֵ��Χ�����������жϣ���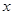 ȡ��ֵʱ��
ȡ��ֵʱ�� ��ֵ������ֵ�Ƕ��٣�
��ֵ������ֵ�Ƕ��٣�
��3������˾Ҫ��֤�����ܵ���4000Ԫ�������۵���x��ȡֵ��ΧΪ����Ԫ���ɽ������κ�����ͼ���𣩣� 
(1) y=-10x+1000��(2) P=-10x2+1500x-50000,6000;(3) 60��x��70.
�������������(1)��֪���㣨60��400���ͣ�70��300�������ô���ϵ�����������y��x�ĺ�����ϵʽ��
��2������������=�����۶�-�ܳɱ������г�P��x֮��ĺ�����ϵʽ���̶���������ֵ��
��3�����������������۵���x��ȡֵ��Χ.
�����������1����y��x�ĺ�����ϵʽΪ��y=kx+b��
�ߺ���ͼ���㣨60��400���ͣ�70��300����
�� �� ���
�� ��� ��
��
��y=-10x+1000��
��2��P="(x-50)(-10x+1000)"
P=-10x2+1500x-50000
�Ա���ȡֵ��Χ��50��x��70��
�� ��
�� ��0��
��0��
�ຯ��P=-10x2+1500x-50000ͼ�����£��Գ�����ֱ��x=75��
��50��x��70����ʱ ��
�� �����������
�����������
�൱x=70ʱ��P���ֵ=6000��
��3����p��4000,��60��x��90,��50��x��70����60��x��70Ԫ.
���㣺1.��һ�κ�����ϵʽ��2.���κ�����Ӧ��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��һ�κ���y��kx��1(k��0)�뷴��������y��(m��0)��ͼ���ڵ�һ�����й�����A(1��2)��ֱ��l��y�ᣮ �ڵ�D(0��3)���뷴����������һ�κ�����ͼ��ֱ��ڵ�B��C��
(1)��һ�κ����뷴���������Ľ���ʽ��
(2)���ABC�������
(3)����ͼ��д����xȡ��ֵʱ��һ�κ�����ֵС�ڷ�����������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�ҹ���һ������ȱˮ�Ĺ��ң�Ϊ�˼�ǿ����Ľ�ˮ��ʶ��ij���ƶ���������ˮ�շѱ���ÿ��ÿ�µ���ˮ������6��ʱ��ˮ��Ϊÿ��2Ԫ������6��ʱ�������IJ��ְ�ÿ��3Ԫ�շѣ�����ij������5�·���ˮx�֣�Ӧ��ˮ��yԪ��
��1����д��y��x�ĺ�����ϵʽ��
��2������û���������½�ˮ��27Ԫ����ô����¸û����˶��ٶ�ˮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ���ڡ�AOB�У���ABO=90�㣬OB=4��AB=8������������y= �ڵ�һ�����ڵ�ͼ��ֱ�OA��AB�ڵ�C�͵�D���ҡ�BOD�����S��BOD=4��
�ڵ�һ�����ڵ�ͼ��ֱ�OA��AB�ڵ�C�͵�D���ҡ�BOD�����S��BOD=4��
��1��������������ʽ��
��2�����C�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
Ϊ�˿�������ڻ���״����һ֧�ƿ�����ij��������һ��һ���Դ�ӪOΪԲ�ģ��뾶Ϊ4km Բ�ο��������߶�P1��P2�DZ����IJ��ֱ߽��ߣ������������߽磩���������ڻ�ʱ���߽����������䴹ֱ�ķ���������ƽ���ƶ�.������n�꣬�����ı߽���P1P2�ƶ��ľ���Ϊs(km),����s��n��nΪ���������Ĺ�ϵ�� .��OΪԭ�㣬������ͼ��ʾ��ƽ��ֱ������ϵ������P1��P2������ֱ��ǣ��C4��9�������C13���C3��.
.��OΪԭ�㣬������ͼ��ʾ��ƽ��ֱ������ϵ������P1��P2������ֱ��ǣ��C4��9�������C13���C3��.
��1�����߶�P1P2���ڵ�ֱ�߶�Ӧ�ĺ�����ϵʽ��
��2��������ı߽����ƶ���������������Ҫ�����ʱ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�ڡ�ĸ�ڡ�����֮�ʣ�ijУ���꼶��֧����֯ȫ����Ա������Ժο��.Ϊ�Oο�ʽ���Ա�����ÿ����ڼ�ȥ���ʻ�����֪��Ա�Ǵӻ��갴ÿ ֧1.5Ԫ�ļ۸�����ʻ��� ֧������ÿ֧5Ԫ�ļ۸�ȫ�����������ӻ��깺���ʻ���ͬʱ������ȥ50Ԫ�����װ���ϣ�
֧������ÿ֧5Ԫ�ļ۸�ȫ�����������ӻ��깺���ʻ���ͬʱ������ȥ50Ԫ�����װ���ϣ�
��1�������O��ο�ʽ�y��Ԫ����x��֧��֮��ĺ�������ʽ��
��2����Ҫ�O������650Ԫ��ο�ʽ�������Ҫ�����ʻ�����֧��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ƽ��ֱ�������У���A������Ϊ��1��1����OA=AC����OAC=90�㣬��DΪx����һ���㣮��ADΪ����AD���Ҳ���������ADEF��
��1������D���߶�OC��ʱ�������O��C�غϣ������߶�CF��OD֮���������ϵΪ ��λ�ù�ϵΪ ��
��2������D���߶�OC���ӳ�����ʱ����1���еĽ����Ƿ����������������˵�����ɣ��������������һ������
��3����D������Ϊ��t��0������D���O���˶���C��ʱ���ú�t�Ĵ���ʽ��ʾE�����꣬��ֱ��д��E����������·������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
���㵺�Թž����й��������й������ѶԵ��㵺��չ��̬��Ѳ��.ij�죬Ϊ���ƻ��㵽��ָ������ijѲ��ͧ�賿1��00������������ʻһ��ʱ�������;���ֹ��ϵ�����һ��ʱ�䣬�����ų���ͧ�ӿ��ٶ�������ǰ�������ǡ���㵽��.��ͼ�Ǹ�ͧ��ʻ��·�� �����������ʱ��t��Сʱ���ĺ���ͼ�����Ѳ��ͧԭ�ƻ��㵽���ʱ���� .
�����������ʱ��t��Сʱ���ĺ���ͼ�����Ѳ��ͧԭ�ƻ��㵽���ʱ���� .
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com