
Ϊ�˿�������ڻ���״����һ֧�ƿ�����ij��������һ��һ���Դ�ӪOΪԲ�ģ��뾶Ϊ4km Բ�ο��������߶�P1��P2�DZ����IJ��ֱ߽��ߣ������������߽磩���������ڻ�ʱ���߽����������䴹ֱ�ķ���������ƽ���ƶ�.������n�꣬�����ı߽���P1P2�ƶ��ľ���Ϊs(km),����s��n��nΪ���������Ĺ�ϵ�� .��OΪԭ�㣬������ͼ��ʾ��ƽ��ֱ������ϵ������P1��P2������ֱ��ǣ��C4��9�������C13���C3��.
.��OΪԭ�㣬������ͼ��ʾ��ƽ��ֱ������ϵ������P1��P2������ֱ��ǣ��C4��9�������C13���C3��.
��1�����߶�P1P2���ڵ�ֱ�߶�Ӧ�ĺ�����ϵʽ��
��2��������ı߽����ƶ���������������Ҫ�����ʱ��.
��1���߶�P1P2���ڵ�ֱ�߶�Ӧ�ĺ�����ϵʽΪ��y=  x+
x+  ��
��
��2�������ı߽����ƶ���������������Ҫ�����ʱ��Ϊ6�꣮
���������������1�����������ϵʽ���ٸ���P1��P2�����꼴�������
��2������������ı߽����ƶ���������������Ҫ����̾���s���ٸ��� �������������n��ֵ���ɣ�
�������������n��ֵ���ɣ�
�����������1�����߶�P1P2���ڵ�ֱ�߶�Ӧ�ĺ�����ϵʽΪ��y=kx+b(k��0)��
����P1��P2������ֱ��ǣ��C4��9�������C13���C3�����У� ��
��
��ã� ��
��
�����߶�P1P2���ڵ�ֱ�߶�Ӧ�ĺ�����ϵʽΪ��y=  x+
x+  ��
��
��2�����߶�P1P2��x����P3���ӳ��߶�P2P1��y����P4��
���߶�P1P2���ڵ�ֱ�߶�Ӧ�ĺ�����ϵʽΪ��y=  x+
x+  ��
��
��P3�� ��0����P4��0��
��0����P4��0�� ����
����
��OP3= ��OP4=
��OP4= ��
��
����O��OH ��P1P2������ΪH��
�� ��
��
�� ��
��
��P1P2���O����ʱ�������ƶ��ľ�����̣���̾���Ϊ��s="OH-4="  -4=
-4=  ��
��
�� ��
��
��ã�n=6����n=-4.8(��ȥ)
�𣺱����ı߽����ƶ���������������Ҫ�����ʱ��Ϊ6�꣮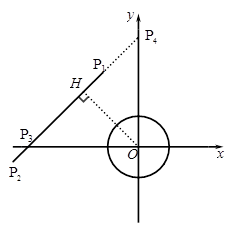 ��
��
���㣺1.һ�κ���2.ֱ����Բ��λ�ù�ϵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��һ�κ��� ��ͼ��ֱ���x�ᡢy�ύ�ڵ�A��B�����߶�ABΪ���ڵ�һ������������Rt��ABC����BAC=90�㣮
��ͼ��ֱ���x�ᡢy�ύ�ڵ�A��B�����߶�ABΪ���ڵ�һ������������Rt��ABC����BAC=90�㣮
��1�����C�����ꣻ
��2����x������һ��P��ʹ����B��C����ľ���֮����С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�ס�����������A��ǰ��B�أ���ͼ�ֱ��ʾ�ס���������A�صľ���S��ǧ�ף���ʱ��t�����ӣ��ĺ�����ϵ.��֪�׳�����10���Ӻ��ҳ��ų������׳���;���ֹͣ��ʻһ��ʱ���ԭ�ټ���ʻ��B�أ����ռס�������ͬʱ����B�أ�����ͼ���ṩ����Ϣ����������⣺
��1���ס���������ʻʱ���ٶȷֱ�Ϊ���٣�
��2���ҳ��������ٷ��Ӻ��һ����׳�������
��3���׳���;�����ֹͣ��ʻ��ʱ��Ϊ���ٷ��ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ij��װ��˾����һ�ֳɱ�Ϊÿ��50Ԫ��T�������涨����ʱ�����۵��۲����ڳɱ��ۣ��ֲ�����ÿ��70Ԫ�������������� �����������۵���
�����������۵���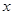 ��Ԫ���Ĺ�ϵ���Խ��ƵĿ���һ�κ�������ͼ����
��Ԫ���Ĺ�ϵ���Խ��ƵĿ���һ�κ�������ͼ����
��1���� ��
��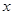 ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2���蹫˾��õ������������� �����۶�
�����۶� �ܳɱ���Ϊ
�ܳɱ���Ϊ Ԫ����
Ԫ���� ��
��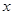 ֮��ĺ�����ϵʽ����д���Ա���
֮��ĺ�����ϵʽ����д���Ա���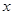 ��ȡֵ��Χ�����������жϣ���
��ȡֵ��Χ�����������жϣ���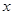 ȡ��ֵʱ��
ȡ��ֵʱ�� ��ֵ������ֵ�Ƕ��٣�
��ֵ������ֵ�Ƕ��٣�
��3������˾Ҫ��֤�����ܵ���4000Ԫ�������۵���x��ȡֵ��ΧΪ����Ԫ���ɽ������κ�����ͼ���𣩣� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ֱ��y=�� x+6��������ֱ���A��B���㣬����P��Qͬʱ��O�������ͬʱ����A�㣬�˶�ֹͣ����Q���߶�OA�˶����ٶ�Ϊÿ��1����λ���ȣ���P��·��O��B��A�˶���
x+6��������ֱ���A��B���㣬����P��Qͬʱ��O�������ͬʱ����A�㣬�˶�ֹͣ����Q���߶�OA�˶����ٶ�Ϊÿ��1����λ���ȣ���P��·��O��B��A�˶���
��1��ֱ��д��A��B��������ꣻ
��2�����Q���˶�ʱ��Ϊt���룩����OPQ�����ΪS�����S��t֮��ĺ�����ϵʽ��
��3����S= ʱ�������P�����꣬��ֱ��д���Ե�O��P��QΪ�����ƽ���ı��εĵ��ĸ�����M�����꣮
ʱ�������P�����꣬��ֱ��д���Ե�O��P��QΪ�����ƽ���ı��εĵ��ĸ�����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ƽ��ֱ������ϵ�У�Rt��PBD��б��PB����y���ϣ�tan��BPD= ���ӳ�BD��x���ڵ�C������D��DA��x�ᣬ����ΪA��OA=4��OB=3��
���ӳ�BD��x���ڵ�C������D��DA��x�ᣬ����ΪA��OA=4��OB=3��
��1�����C�����ꣻ
��2������D�ڷ���������y= ��k��0����ͼ���ϣ����������Ľ���ʽ��
��k��0����ͼ���ϣ����������Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��ֱ��y=mx��˫����y= �ཻ��A��B���㣬A�������Ϊ��1��2��
�ཻ��A��B���㣬A�������Ϊ��1��2��
��1�����������ı���ʽ��
��2������ͼ��ֱ��д����mx�� ʱ��x��ȡֵ��Χ��
ʱ��x��ȡֵ��Χ��
��3�������߶�AB�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�졢�������ֱ�����360ǧ��·�̵ļס�������ͬʱ������������ʻ����������У��쳵�����ҵغ�ͣ��1Сʱ��Ȼ��ԭ·ԭ�ٷ��أ��쳵��������1Сʱ����أ��졢����������Գ����ص�·��y(ǧ��)����������õ�ʱ��x(Сʱ)�Ĺ�ϵ��ͼ��ʾ��
����ͼ����Ϣ����������⣺
(1)�������ٶ��� ǧ�ף�Сʱ���쳵���ٶ��� ǧ�ף�Сʱ��
(2)��m��ֵ����ָ����C��ʵ��������ʲô��
(3)�ڿ쳵��ԭ·ԭ�ٷ��صĹ����У��졢����������·��Ϊ150ǧ��ʱ��������ʻ�˶���Сʱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪����ͼ������������ ��һ�κ���
��һ�κ��� ��ͼ����A��3,1����B��m��-3������.
��ͼ����A��3,1����B��m��-3������.
��1���������� ��һ�κ���
��һ�κ��� �Ľ���ʽ.
�Ľ���ʽ.
��2������P��ֱ�� ��һ�㣬��OP=
��һ�㣬��OP= OA����ֱ��д����P������.
OA����ֱ��д����P������.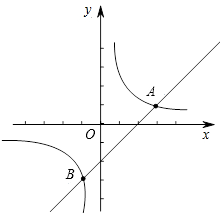
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com