解:(1)分两种情况:
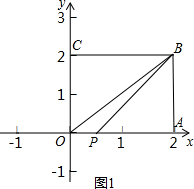
①当点P在线段OA上运动时,如图1,
y=

x×2,
即y=x,0<x≤2;
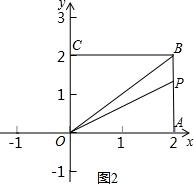
②当点P在线段AB上运动时(不含点A),如图2,
y=

(4-x)×2,
即y=-x+4,2<x<4;
(2)由题意可知:
①

=x,
此时,点P(

,0),
②

=-x+4,
x=

,
x-2=

.
此时,点P(2,

),
综合(2)中的①,②可得P(

,0)或P(2,

);
(3)如图3,存在满足条件的直线.
设这条直线的解析式为y=kx-1,
由于直线平分正方形OABC的面积,可得:OM=BN,延长AB,交直线与点H,
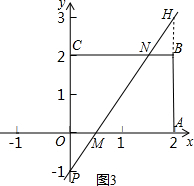
∵△POM≌△HBN,
∴BH=OP=1,
∴H(2,3),
由点H在直线上,得3=2k-1,
∴k=2,
∴所求直线的解析式为y=2x-1,
另法:由直线平分正方形AOCB的面积,
可知,直线过正方形AOCB的中心.
∴直线过(1,1)点,
∴直线的解析式为y=2x-1.
分析:(1)根据三角形面积公式建立起x和y之间的函数关系式,并分点P在线段OA上运动时和点P在线段AB上运动时(不含点A)两种情况讨论;(2)将y=

代入求值即可;(3)先画出图形进行猜想,然后利用三角形相似或正方形的对称性求出直线所经过的点,进而求出解析式.
点评:此题将一次函数和正方形、三角形相结合并具有一定的开放性,考查了同学们对三角形面积公式、正方形的性质以及一次函数的性质的认识,有利于培养同学们的探索发现意识和严密的数学思维习惯.

 着正方形的边,按O→A→B的顺序运动,设点P经过的路程为x,△OPB的面积为y.
着正方形的边,按O→A→B的顺序运动,设点P经过的路程为x,△OPB的面积为y.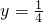 时,点P的坐标;
时,点P的坐标; 解:(1)分两种情况:
解:(1)分两种情况: x×2,
x×2, (4-x)×2,
(4-x)×2,
 =x,
=x, ,0),
,0), =-x+4,
=-x+4, ,
, .
. ),
), ,0)或P(2,
,0)或P(2, );
);
 代入求值即可;(3)先画出图形进行猜想,然后利用三角形相似或正方形的对称性求出直线所经过的点,进而求出解析式.
代入求值即可;(3)先画出图形进行猜想,然后利用三角形相似或正方形的对称性求出直线所经过的点,进而求出解析式.

 阅读快车系列答案
阅读快车系列答案 的垂线,垂足分别为E、F,并设矩形OEPF和正方形OABC不重合部分的面积为S.(提示:考虑点P在点B的左侧或右侧两种情况)
的垂线,垂足分别为E、F,并设矩形OEPF和正方形OABC不重合部分的面积为S.(提示:考虑点P在点B的左侧或右侧两种情况) 如图,正方形OABC、ADEF的顶点A,D,C在坐标轴上,点F在AB上,点B、E在函数y=
如图,正方形OABC、ADEF的顶点A,D,C在坐标轴上,点F在AB上,点B、E在函数y= 如图,正方形OABC和正方形ADEF的顶点A,D,C在坐标轴上,点F在AB上,点B,E在函数y=
如图,正方形OABC和正方形ADEF的顶点A,D,C在坐标轴上,点F在AB上,点B,E在函数y= 如图,正方形OABC与正方形ODEF是位似图形,O为位似中心,相似比为1:
如图,正方形OABC与正方形ODEF是位似图形,O为位似中心,相似比为1: 象上,点P(m,n)是函数y=
象上,点P(m,n)是函数y=