

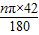 =16π,
=16π, ,由y≥0,得x的最大值是
,由y≥0,得x的最大值是 ,最小值是0.
,最小值是0. ;x=2时,y=6;x=3时,
;x=2时,y=6;x=3时, ;
; x=5时,y=2;x=6时,
x=5时,y=2;x=6时,

 DC=
DC= ×79=39.5,又CP=42,
×79=39.5,又CP=42, ,
,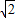 ,所以这样的裁剪草图是可行的.
,所以这样的裁剪草图是可行的.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
某外语学校在圣诞节要举行汇报演出,需要准备一些圣诞帽,为了培养学生的动手能力,学校决定自己制作这些圣诞帽.如果圣诞帽(圆锥形状)的规格是母线长42厘米,底面直径为16厘米.
⑴ 求圣诞帽的侧面展开图(扇形)的圆心角的度数(精确到度);
⑵ 已知A种规格的纸片能做3个圣诞帽,B种规格的纸片能做4个圣诞帽,汇报演出需要26个圣诞帽,写出A种规格的纸片y张与B种规格的纸片x张之间的函数关系式及其x的最大值与最小值;若自己制作时,A、B两种规格的纸片各买多少张时,才不会浪费纸张?
 ⑶ 现有一张边长为79厘米的正方形纸片,它最多能制作几个这种规格的圣诞帽(圣诞帽的粘接处忽略不计).请在比例尺为1:15的正方形纸片上画出圣诞帽的侧面展开图的裁剪草图,并利用所学的数学知识说明其可行性.
⑶ 现有一张边长为79厘米的正方形纸片,它最多能制作几个这种规格的圣诞帽(圣诞帽的粘接处忽略不计).请在比例尺为1:15的正方形纸片上画出圣诞帽的侧面展开图的裁剪草图,并利用所学的数学知识说明其可行性.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
某外语学校在圣诞节要举行汇报演出,需要准备一些圣诞帽,为了培养学生的动手能力,学校决定自己制作这些圣诞帽.如果圣诞帽(圆锥形状)的规格是母线长42厘米,底面直径为16厘米.
⑴ 求圣诞帽的侧面展开图(扇形)的圆心角的度数(精确到度);
⑵ 已知A种规格的纸片能做3个圣诞帽,B种规格的纸片能做4个圣诞帽,汇报演出需要26个圣诞帽,写出A种规格的纸片y张与B种规格的纸片x张之间的函数关系式及其x的最大值与最小值;若自己制作时,A、B两种规格的纸片各买多少张时,才不会浪费纸张?
 ⑶ 现有一张边长为79厘米的正方形纸片,它最多能制作几个这种规格的圣诞帽(圣诞帽的粘接处忽略不计).请在比例尺为1:15的正方形纸片上画出圣诞帽的侧面展开图的裁剪草图,并利用所学的数学知识说明其可行性.
⑶ 现有一张边长为79厘米的正方形纸片,它最多能制作几个这种规格的圣诞帽(圣诞帽的粘接处忽略不计).请在比例尺为1:15的正方形纸片上画出圣诞帽的侧面展开图的裁剪草图,并利用所学的数学知识说明其可行性.
 |
查看答案和解析>>
科目:初中数学 来源:2012年广东省华师附中实验学校中考数学模拟试卷(一)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com