
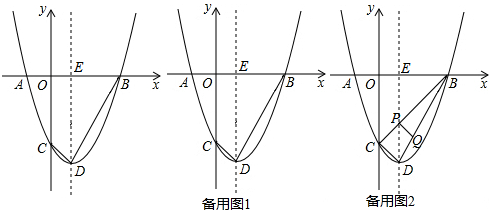
���� ��1������A��B���ڶԳ���Ϊx=1�Գƣ���A��-1��0�����õ�B��3��0��������-1��3�Ƿ���ax2+bx-3=0�ĸ����õ�-1+3=-$\frac{b}{a}$�����a=1��b=-2������������y=x2-2x-3����x=1ʱ��y=-4������ȷ��D��1��-4����
��2������N������CD�ϣ��籸��ͼ1-1���ӳ�MN��y���ڵ�F������M��MG��y���ڵ�G����֤��MCN�ס�DBE���õ�MN=2CN����CN=a����MN=2a�����MG=FG=$\frac{3\sqrt{2}}{2}$a��CG=FG-FC=$\frac{\sqrt{2}}{2}$a������������y=��x-3����x+1�������a��ֵ������֪M�����ꣻ����N������DC�ϣ��籸��ͼ1-2��MN��y���ڵ�F������M��MG��y���ڵ�G�������Ƶķ������a��ֵ��ȷ��M�����ꣻ
��3��������������𣬻���ͼ�Σ����ý������Σ����ɽ��
��� �⣺��1����A��B���ڶԳ���Ϊx=1�Գƣ���A��-1��0����
��B��3��0����
��-1��3�Ƿ���ax2+bx-3=0�ĸ���
��-1+3=-$\frac{b}{a}$��
��ã�a=1��b=-2��
��������y=x2-2x-3��
��y=x2-2x-3=��x-1��2-4��
�ඥ��D������Ϊ��1��-4����
��2��������N������CD�ϣ��籸��ͼ1-1���ӳ�MN��y���ڵ�F������M��MG��y���ڵ�G��
�ߡ�CMN=��BDE����CNM=��BED=90�㣬
���MCN�ס�DBE��
��$\frac{CN}{MN}$=$\frac{BE}{DE}$=$\frac{1}{2}$��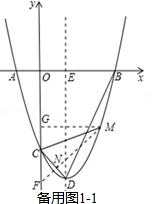
��MN=2CN��
��CN=a����MN=2a��
�ߡ�CDE=��DCF=45�㣬
���CNF����MGF��Ϊ����ֱ�������Σ�
��NF=CN=a��CF=$\sqrt{2}$a��
��MF=MN+NF=3a��
��MG=FG=$\frac{3\sqrt{2}}{2}$a��
��CG=FG-FC=$\frac{\sqrt{2}}{2}$a��
��M��$\frac{3\sqrt{2}}{2}$a��-3+$\frac{\sqrt{2}}{2}$a���� 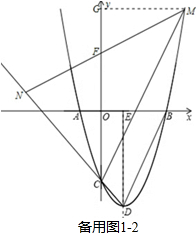
����������y=��x-3����x+1�������a=$\frac{7\sqrt{2}}{9}$��
��M��$\frac{7}{3}$��-$\frac{20}{9}$����
������N������DC�ϣ��籸��ͼ1-2��MN��y���ڵ�F������M��MG��y���ڵ�G��
�ߡ�CMN=��BDE����CNM=��BED=90�㣬
���MCN�ס�DBE
��$\frac{CN}{MN}$=$\frac{BE}{DE}$=$\frac{1}{2}$��
��MN=2CN��
��CN=a����MN=2a��
�ߡ�CDE=45�㣬
���CNF����MGF��Ϊ����ֱ�������Σ�
��NF=CN=a��CF=$\sqrt{2}$a��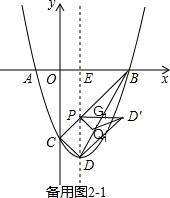
��MF=MN-NF=a��
��MG=FG=$\frac{\sqrt{2}}{2}$a��
��CG=FG+FC=$\frac{3\sqrt{2}}{2}$a��
��M��$\frac{\sqrt{2}}{2}$a��-3+$\frac{3\sqrt{2}}{2}$a����
����������y=��x-3����x+1�������a=5$\sqrt{2}$��
��M��5��12����
���Ͽ�֪����M����Ϊ��$\frac{7}{3}$��-$\frac{20}{9}$����5��12����
��3���籸��ͼ2-1��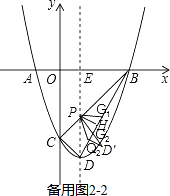
��֪PG1�ǡ�DBE����λ�ߣ�PQ1ƽ�֡�DPD����
���DPQ1=45�㣬
Rt��DBE�����߱�Ϊ1��2��$\sqrt{5}$��
��tan��EDB=$\frac{1}{2}$��
���PDQ1�ã�DQ1=$\frac{\sqrt{5}}{3}$PD=$\frac{2\sqrt{5}}{3}$��
��ʱt=$\frac{2}{3}$��
�籸��ͼ2-2��
��PH��BD��PG1��PG2����PH�Գƣ�PQ2ƽ�֡�DPQ2��
�á�Q2PH=45�㣬
�������ε�DQ2=$\frac{2\sqrt{5}}{5}$��
��ʱt=$\frac{2}{5}$��
��t=$\frac{2}{3}$��t=$\frac{2}{5}$��
���� ���⿼���˶��κ�����Ӧ�á����ɶ����涨�������������ε����ʺ��ж����ر�ע���������ν�����ⲿ�ֿ�����ص㣬Ҳ���ѵ㣮�ڣ�3����ע���������˼���Ӧ�ã�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
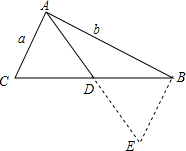 ��ͼ��ʾ��������������֪����֮���ֱ�Ϊa��b��a��b������ô�������ϵ����ߵij���x��ȡֵ��Χ��$\frac{b-a}{2}$��x��$\frac{b+a}{2}$��
��ͼ��ʾ��������������֪����֮���ֱ�Ϊa��b��a��b������ô�������ϵ����ߵij���x��ȡֵ��Χ��$\frac{b-a}{2}$��x��$\frac{b+a}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
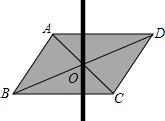 ��Ӳֽ���һ��ƽ���ı��Σ��������ĶԽ��ߵĽ���O���ô�ͷ���һ��ƽ����ƽ���ı����ϵ�ֱϸľ���̶��ڵ�O������ľ����AD���ڵ�E����BC���ڵ�F������ϸľ��
��Ӳֽ���һ��ƽ���ı��Σ��������ĶԽ��ߵĽ���O���ô�ͷ���һ��ƽ����ƽ���ı����ϵ�ֱϸľ���̶��ڵ�O������ľ����AD���ڵ�E����BC���ڵ�F������ϸľ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6�� | B�� | 5�� | C�� | 4�� | D�� | 3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
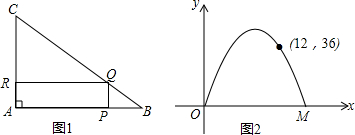
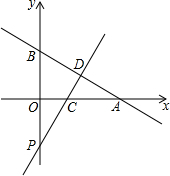 ��ͼ��һ�κ���y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$��ͼ����������ֱ��ڵ�A��B���㣬����AOB��ֱ��CD����ʹ��A���B�غϣ�ֱ��CD��AB�ڵ�D��
��ͼ��һ�κ���y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$��ͼ����������ֱ��ڵ�A��B���㣬����AOB��ֱ��CD����ʹ��A���B�غϣ�ֱ��CD��AB�ڵ�D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com