练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】先化简再求值，（3a﹣2）2﹣3a（2a﹣1）+5，其中a是方程x2﹣3x+1＝0的解．

    【答案】3a2﹣9a+9，6

    【解析】

    根据完全平方公式以及整式的混合运算法则，先化简，再代入求值，即可得到答案．

    原式＝9a2﹣12a+4﹣6a2+3a+5

    ＝3a2﹣9a+9，

    把x＝a代入方程得：a2﹣3a+1＝0，即a2﹣3a＝﹣1，

    ∴原式＝3a2﹣9a+9＝3（a2﹣3a）+9=﹣3+9＝6．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】解方程：2m（3m﹣5）+3m（1﹣2m）=14．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算:9n+2÷9n=_________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算:-2x2y3·7xyz=___________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【探索新知】

    如图1，射线OC在∠AOB的内部，图中共有3个角：∠AOB、∠AOC和∠BOC，若其中有一个角的度数是另一个角度数的两倍，则称射线OC是∠AOB的“妙分线”．

    【解决问题】

    （1）如图2，若∠MPN= ，且射线PQ是∠MPN的“妙分线”，则∠NPQ= ____ ．（用含的代数式表示出所有可能的结果）

    【深入研究】

    如图2，若∠MPN=54°，且射线PQ绕点P从PN位置开始，以每秒8°的速度顺时针旋转，当PQ与PN成时停止旋转，旋转的时间为t秒．

    （2）当t为何值时，射线PM是∠QPN的“妙分线”．

    （3）若射线PM同时绕点P以每秒6°的速度顺时针旋转，并与PQ同时停止．请求出当射线PQ 是∠MPN的“妙分线”时t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，BA=BC，以AB为直径的⊙O分别交AC、BC于点D、E，BC的延长线于⊙O的切线AF交于点F．

    （1）求证：∠ABC=2∠CAF；

    （2）若AC=2，CE：EB=1：4，求CE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知A样本的数据如下：72，73，76，76，77，78，78，78，B样本的数据恰好是A样本数据每个都加2，则A，B两个样本的下列统计量对应相同的是（ ）
    A.平均数
    B.标准差
    C.中位数
    D.众数

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知在四边形ABCD中，AB=20cm，BC=15cm，CD=7cm，AD=24cm，∠ABC=90°．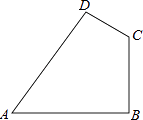

    （1）猜想的∠A与∠C关系；
    （2）求出四边形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】A校女生占全校总人数的40%，B校女生占全校总人数的55%，则女生人数（　　）
    A.A校多于B校
    B.A校与B校一样多
    C.A校少于B校
    D.不能确定

    查看答案和解析>>

    同步练习册答案