
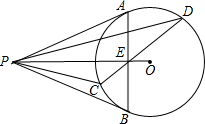
 如图,已知P为⊙O外一点,PA切⊙O于点A,PB切⊙O于点B,AB交OP于点E,弦CD过E点.求证:∠APC=∠BPD.
如图,已知P为⊙O外一点,PA切⊙O于点A,PB切⊙O于点B,AB交OP于点E,弦CD过E点.求证:∠APC=∠BPD. 分析 连结OA、OC、OD,如图,利用切线长定理得PA=PB,∠APO=∠BPO,而OA=OB,可判断PO垂直平分AB,再根据切线的性质得OA⊥PA,加上∠AOE=∠POA,则可判断Rt△OAE∽Rt△OPA,得到OA:OE=OP:OA,即OA2=OE•OP,由于OC=OD=OA,所以OC2=OE•OP,OD2=OE•OP,加上∠COE=∠POC,所以△OCE∽△OPC,根据相似的性质得∠OCD=∠2,同理可得∠ODC=∠1,而∠OCD=∠ODC,则∠1=∠2,从而可得∠APC=∠BPD.
解答 证明:连结OA、OC、OD,如图,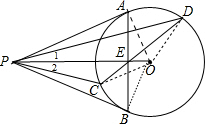
∵PA切⊙O于点A,PB切⊙O于点B,
∴PA=PB,
而OA=OB,
∴PO垂直平分AB,
∴∠APO=∠BPO,
∵PA切⊙O于点A,
∴OA⊥PA,
而∠AOE=∠POA,
∴Rt△OAE∽Rt△OPA,
∴OA:OE=OP:OA,
∴OA2=OE•OP,
∵OC=OD=OA,
∴OC2=OE•OP,OD2=OE•OP,
而∠COE=∠POC,
∴△OCE∽△OPC,
∴∠OCD=∠2,
同理得△ODE∽△OPD,
∴∠ODC=∠1,
而OC=OD,
∴∠OCD=∠ODC,
∴∠1=∠2,
∴∠APO+∠2=∠BPO+∠1,
即∠APC=∠BPD.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了相似三角形的判定与性质.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{9}$ | B. | $\root{3}{8}$ | C. | $\frac{π}{2}$ | D. | 2.020020002 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com