练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在中，是角平分线，，

    （1）求的度数．

    （2）过点作边上的高， 垂足为；求的度数．

    【答案】（1）∠BAD=35°；（2）∠EAD=15°．

    【解析】

    （1）根据三角形内角和定理求出∠BAC的度数，根据角平分线得定义即可求出∠BAD的度数；

    （2）由直角三角形两锐角互余的关系可求出∠CAE的度数，根据角平分线的定义可求出∠CAD的度数，根据角的和差关系即可求出∠EAD的度数．

    （1）∵∠B=40°，∠C=70°，∠BAC+∠B+∠C=180°，

    ∴∠BAC=180°-∠B-∠C=70°，

    ∵是角平分线，

    ∴∠BAD=∠CAD=∠BAC=35°．

    （2）∵AE为BC边上的高，

    ∴∠AEC=90°，

    ∵∠C=70°，

    ∴∠CAE=90°-∠C=20°，

    ∵∠CAD=35°，

    ∴∠EAD=∠CAD-∠CAE=15°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD中，∠B=90°，AB∥CD，M为BC边上的一点，且AM平分∠BAD，DM平分∠ADC．

    求证：（1）AM⊥DM；

    （2）M为BC的中点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD中，∠A=∠C=90°，BE，DF分别是∠ABC，∠ADC的平分线．

    （1）∠1与∠2有什么关系，为什么？

    （2）BE与DF有什么关系？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,已知A,D,E三点共线,C,B,F三点共线,AB=CD,AD=CB,DE=BF,那么BE与DF之间有什么数量关系?请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：
    （1）（﹣3）2﹣（+4 ）+（﹣1 ）
    （2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一辆汽车在直线形的公路上由A向B行驶，M、N分别是位于公路AB两侧的两个学校，如图.

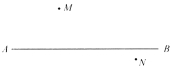
    (1)汽车行驶时，会对公路两旁的学校都造成一定的影响，当汽车行驶到何处时，分别对两个学校影响最大?在图中标出来；

    (2)当汽车从A向B行驶时，在哪一段上对两个学校影响越来越大?越来越小?对M学校影响逐渐减小而对N学校影响逐渐增大?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线AB、CD相交于点O，OM⊥AB．

    （1）若∠1=∠2，求∠NOD．

    （2）若∠1=∠BOC，求∠AOC与∠MOD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】三角形ABC的三条内角平分线为AE、BF、CG，下面的说法中正确的个数有（ ）

    ①△ABC的内角平分线上的点到三边距离相等

    ②三角形的三条内角平分线交于一点

    ③三角形的内角平分线位于三角形的内部

    ④三角形的任一内角平分线将三角形分成面积相等的两部分．

    A.1个B.2个C.3个D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O的半径OD⊥弦AB于点C，连结AO并延长交⊙O于点E，连结EC．若AB=8，CD=2，则sin∠ECB为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    同步练习册答案