
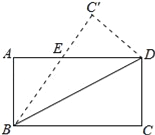
【题目】如图,在矩形ABCD中,BC=6cm,CD=3cm,将△BCD沿BD翻折,点C落在点C′处,BC′交AD于点E,则AE的长为______ cm.
【答案】![]()
【解析】根据翻折的性质可得∠BCD=∠EBD,再根据两直线平行,内错角相等可得∠BCD=∠ADB,从而得到∠EBD=∠ADB,然后根据等角对等边可得BE=DE,再根据矩形的对边相等可得AB=CD,AD=BC,设AE=x,表示出BE,然后在Rt△ABE中,利用勾股定理列出方程求解即可.
解:∵△BCD沿BD翻折,点C落在点C′处,
∴∠BCD=∠EBD,
∵矩形的对边AD∥BC,
∴∠BCD=∠ADB,
∴∠EBD=∠ADB,
∴BE=DE,
在矩形ABCD中,AB=CD=3cm,AD=BC=6cm,
设AE=xcm,则BE=DE=AD﹣AE=6﹣x,
在Rt△ABE中,由勾股定理得,AB2+AE2=BE2,
即32+x2=(6﹣x)2,
解得x=![]() ,
,
即AE=![]() cm.
cm.
故答案为: ![]() .
.
“点睛”本题考查了翻折变换的性质,矩形的性质,平行四边形的性质,等角对等边的性质,难点在于将所求的边以及已知的边的长度转化到同一个直角三角形中利用勾股定理列出方程.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
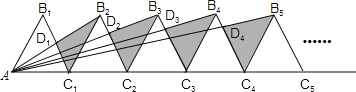
【题目】如图,n+1个边长为2的等边三角形有一条边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面积为S2,…,△Bn+1DnCn的面积为Sn,则S2= ;Sn= .(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
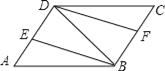
【题目】如图,在ABCD中,连接对角线BD,BE平分∠ABD交AD于点E,DF平分∠BDC交BC于点F.
(1)求证:△AEB≌△CFD;
(2)若BD=BA,试判断四边形DEBF的形状,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
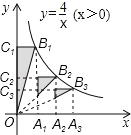
【题目】如图,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数![]() 的图象分别交于点B1、B2、B3,分别过点B1、B2、B3作x轴的平行线,分别与y轴交于点C1、C2、C3,连结OB1、OB2、OB3,那么图中阴影部分的面积之和为 .
的图象分别交于点B1、B2、B3,分别过点B1、B2、B3作x轴的平行线,分别与y轴交于点C1、C2、C3,连结OB1、OB2、OB3,那么图中阴影部分的面积之和为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 对角线互相垂直的四边形是菱形 B. 矩形的对角线互相垂直
C. 一组对边平行的四边形是平行四边形 D. 四边相等的四边形是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列从左到右的变形,属于因式分解的是( )
A. (x+3)(x-2)=x2+x-6 B. ax-ay-1=a(x-y)-1
C. 6a2b3=2a2·3b3 D. x2-4x+4=(x-2)2
查看答案和解析>>
科目:初中数学 来源: 题型:
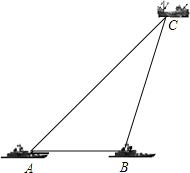
【题目】如图,在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持10海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一不明国籍的渔船C,求此时渔船C与海监船B的距离是多少.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com