
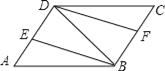
【题目】如图,在ABCD中,连接对角线BD,BE平分∠ABD交AD于点E,DF平分∠BDC交BC于点F.
(1)求证:△AEB≌△CFD;
(2)若BD=BA,试判断四边形DEBF的形状,并加以证明.
【答案】(1)证明见解析;(2)四边形DEBF是矩形;理由见解析.
【解析】分析:(1)由平行四边形的性质得出AD∥BC,CD∥BA,∠A=∠C,AB=CD,得出∠ABD=∠BDC,由角平分线的定义证出∠DBE=∠FDB,由ASA证明△AEB≌△CFD即可;(2)先证明四边形DEBF是平行四边形,再根据等腰三角形的“三线合一”的性质推知BE⊥AD,然后由“有一内角为直角的平行四边形是矩形”证得四边形DEBF是矩形即可.
本题解析:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,CD∥BA,∠A=∠C,AB=CD,
∴∠ABD=∠BDC(两直线平行,内错角相等).
又∵BE平分∠ABD,DF平分∠BDC,
∴∠ABE=∠DBE=![]() ∠ABD,∠CDF=∠BDF=
∠ABD,∠CDF=∠BDF=![]() ∠BDC,
∠BDC,
∴∠DBE=∠FDB=∠DBE=∠BDF(等量代换),
在△AEB和△CFD中, 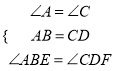 ,
,
∴△AEB≌△CFD(ASA);
(2)解:四边形DEBF是矩形;理由如下:
由(1)知:∠DBE=∠BDF,
∴BE∥DF,
∵DE∥BF,
∴四边形EBFD是平行四边形.
∵BD=BA,BE是∠ABD的平分线,
∴BE⊥AD,
∴∠DEB=90°,
∴四边形DEBF是矩形(有一内角为直角的平行四边形是矩形).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图 1,二次函数![]() 的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
(1)求二次函数![]() 的表达式;
的表达式;
(2)连接 BC ,当t=![]() 时,求△BCP的面积;
时,求△BCP的面积;
(3)如图 2,动点 P 从 A 出发时,动点 Q 同时从 O 出发,在线段 OA 上沿 O→A 的方向以 1个单位长度的速度运动,当点 P 与 B 重合时,P 、 Q 两点同时停止运动,连接 DQ 、 PQ ,将△DPQ沿直线 PC 折叠到 △DPE .在运动过程中,设 △DPE 和 △OAB重合部分的面积为 S ,直接写出 S 与 t 的函数关系式及 t 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
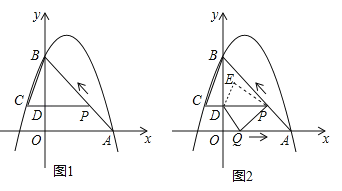
【题目】如图1,滨海广场装有风能、太阳能发电的风光互补环保路灯,灯杆顶端装有风力发电机,中间装有太阳能板,下端装有路灯.该系统工作过程中某一时刻的截面图如图2,已知太阳能板的支架BC垂直于灯杆OF,路灯顶端E距离地面6米,DE=1.8米,∠CDE=60°.且根据我市的地理位置设定太阳能板AB的倾斜角为43°.AB=1.5米,CD=1米,为保证长为1米的风力发电机叶片无障碍安全旋转,对叶片与太阳能板顶端A的最近距离不得少于0.5米,求灯杆OF至少要多高?(利用科学计算器可求得sin43°≈0.6820,cos43°≈0.7314,tan43°≈0.9325,结果保留两位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:●和○两种圆按某种规则排列,则前2017个圆中有○ 个.( )
○●○●●○●●●○●○●●○●●●○●○●●○●●●……
A. 671 B. 672 C. 673 D. 674
查看答案和解析>>
科目:初中数学 来源: 题型:
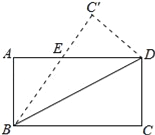
【题目】如图,在矩形ABCD中,BC=6cm,CD=3cm,将△BCD沿BD翻折,点C落在点C′处,BC′交AD于点E,则AE的长为______ cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列因式分解中,是利用提公因式法分解的是( )
A. a2﹣b2=(a+b)(a﹣b) B. a2﹣2ab+b2=(a﹣b)2
C. ab+ac=a(b+c) D. a2+2ab+b2=(a+b)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com