
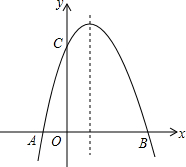
 已知,二次函数y=ax2-2ax+b的图象与x轴交于A,B两点,与y轴交于C点,且OB=OC=3.
已知,二次函数y=ax2-2ax+b的图象与x轴交于A,B两点,与y轴交于C点,且OB=OC=3.分析 (1)先确定B点和C点坐标,然后把它们代入y=ax2-2ax+b中得到关于a、b的方程组,然后解方程组即可;
(2)先计算出抛物线的对称轴方程和A点坐标,再利用两点之间线段最短作出四边形ACMN的周长最短的图形,如图,则利用待定系数法求出PB的解析式,则可得到N点坐标,同时也可得到M点坐标,然后计算AC和PB的长可得到四边形ACMN的周长最小值.
解答 解:(1)∵OB=OC=3,
∴B(3,0),C(0,3),
把B(3,0),C(0,3)代入y=ax2-2ax+b得$\left\{\begin{array}{l}{9a-6a+b=0}\\{b=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-1}\\{b=3}\end{array}\right.$.
∴二次函数的解析式为y=-x2+2x+3;
(2)如图,抛物线的对称轴为直线x=-$\frac{2}{2×(-1)}$=1,
则A(-1,0),
在y轴截取CP=MN=1,连结BP交直线x=1于N,连结CM,
∵点A与点B关于直线x=1对称,
∴NA=NB,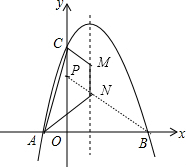
∵PC=MN,PC∥MN,
∴四边形MCPN为平行四边形,
∴CM=PN,
∴CM+NA=PN+NB=PB,
∴此时四边形ACMN的周长最短,
设直线PB的解析式为y=kx+q,
把P(0,2),B(3,0)代入得$\left\{\begin{array}{l}{q=2}\\{3k+q=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{2}{3}}\\{q=2}\end{array}\right.$,
∴直线PB的解析式为y=-$\frac{2}{3}$x+2,
当x=1时,y=-$\frac{2}{3}$x+2=$\frac{4}{3}$,则N(1,$\frac{4}{3}$),M(1,$\frac{7}{3}$),
∵AC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,PB=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
∴四边形ACMN的周长最小值为$\sqrt{10}$+$\sqrt{13}$+1.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题化为解关于x的一元二次方程.本题的难点是作出四边形ACMN的周长最短的图形.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 互为相反数的两个数的绝对值一定相等 | |
| B. | 绝对值最小的数是0 | |
| C. | 符号不同的两个数互为相反数 | |
| D. | 任何有理数都可以用数轴上的点表示 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
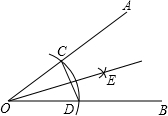 小明同学画角平分,作法如下:
小明同学画角平分,作法如下:| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2020 | B. | 2 | C. | $\frac{1}{2}$ | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com