

分析 (1)、Ⅰ)、求简单的线段相等,可证线段所在的三角形全等,即连接EF,证△EGF≌△EDF即可;
Ⅱ)、可设DF=x,BC=y;进而可用x表示出DC、AB的长,根据折叠的性质知AB=BG,即可得到BG的表达式,由(1)证得GF=DF,那么GF=x,由此可求出BF的表达式,进而可在Rt△BFC中,根据勾股定理求出x、y的比例关系,即可得到$\frac{AD}{AB}$的值,代值即可得出结论;
(2)方法同(2).
解答 解:(1)、
Ⅰ)、连接EF,
根据翻折的性质得,∠EGF=∠D=90°,
EG=AE=ED,EF=EF,
在Rt△EGF和Rt△EDF中,$\left\{\begin{array}{l}{EG=ED}\\{EF=EF}\end{array}\right.$,
∴Rt△EGF≌Rt△EDF(HL),
∴GF=DF;
Ⅱ)由(1)知,GF=DF,设DF=x,BC=y,则有GF=x,AD=y
∵DC=2DF,
∴CF=x,DC=AB=BG=2x,
∴BF=BG+GF=3x;
在Rt△BCF中,BC2+CF2=BF2,即y2+x2=(3x)2
∴y=2$\sqrt{2}$x,
∴$\frac{AD}{AB}=\frac{y}{2x}$=$\sqrt{2}$;
∵AD=4,
∴AB=2$\sqrt{2}$
(3)由(1)知,GF=DF,设DF=x,BC=y,则有GF=x,AD=y
∵DC=k•DF,
∴BF=BG+GF=(k+1)x
在Rt△BCF中,BC2+CF2=BF2,
即y2+[(k-1)x]2=[(k+1)x]2
∴y=2x$\sqrt{k}$,
∴$\frac{AD}{AB}=\frac{y}{kx}$=$\frac{2\sqrt{k}}{k}$.
点评 此题是折叠问题,主要考查了矩形的性质、图形的折叠变换、全等三角形的判定和性质、勾股定理的应用等重要知识,难度适中.用勾股定理表示出y是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
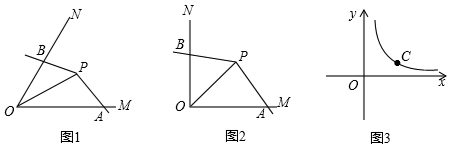 如图1,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足OA•OB=OP2,我们就把∠APB叫做∠MON的智慧角.
如图1,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足OA•OB=OP2,我们就把∠APB叫做∠MON的智慧角.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 八年级(3)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学在制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20cm,宽AB=16cm的矩形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处,则EC的长为6 cm.
八年级(3)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学在制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20cm,宽AB=16cm的矩形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处,则EC的长为6 cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com