
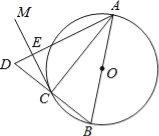
【题目】如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.
(1)求证:∠ACM=∠ABC;
(2)延长BC到D,使CD=BC,连接AD与CM交于点E,若⊙O的半径为2,ED=1,求AC的长.
【答案】(1)证明参见解析;(2)2![]() .
.
【解析】
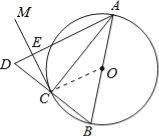
试题分析:(1)连接OC,由∠ABC+∠BAC=90°及CM是⊙O的切线得出∠ACM+∠ACO=90°,再利用∠BAC=∠ACO,得出结论,(2)连接OC,得出△AEC是直角三角形,△AEC的外接圆的直径是AC,利用△ABC∽△CDE,求出AC.
试题解析:(1)连接OC.∵AB为⊙O的直径,∴∠ACB=90°.∴∠ABC+∠BAC=90°.∵CM是⊙O的切线,∴OC⊥CM.∴∠ACM+∠ACO=90°.∵CO=AO,∴∠BAC=∠ACO.∴∠ACM=∠ABC.(2)∵BC=CD,OB=OA,∴OC∥AD.又∵OC⊥CE,∴CE⊥AD,∵∠ACD=∠ACB=90°,∴∠AEC=∠ACD.∴△ADC∽△ACE.∴![]() .∵⊙O的半径为2,∴AD=4.∴
.∵⊙O的半径为2,∴AD=4.∴![]() .∴AC=2
.∴AC=2![]() .
.


科目:初中数学 来源: 题型:
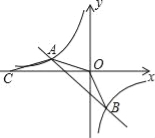
【题目】如图,直线AB与反比例函数的图象交于A(﹣4,m)、B(2,n)两点,点C在x轴上,AO=AC,△OAC的面积为8.
(1)求反比例函数的解析式.
(2)求cos∠OBA的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
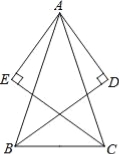
【题目】如图,在△ABC中,AB=AC,BD平分∠ABC,CE平分∠ACB,过点A分别作BD、CE的垂线段AD、AE,垂足为D、E,求证:AD=AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF、CE,且∠FBD=35°,∠BDF=75°,下列说法:①△BDF≌CDE;②ABD和△ACD面积相等;③BF∥CE;④∠DEC=70°,其中正确的有( ) 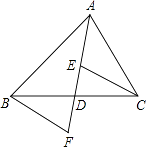
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市自来水公司收费标准如下:每月每户用水不超过8吨的部分按0.5元/吨收费;超过8吨而不超过20吨的部分按1元/吨收费;超过20吨的部分按1.6元/吨收费.小明家12月份缴水费24元,则他家该月用水( )吨.
A. 25 B. 30 C. 48 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象过点(﹣1,2)且与x轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:①4a﹣2b+c<0;②2a﹣b<0;③b2+8a>4ac;④abc>0,其中正确的有( ).
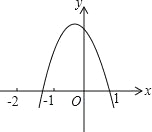
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
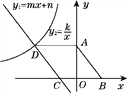
【题目】如图,在菱形ABCD中,AD∥x轴,点A的坐标为(0,4),点B的坐标为(3,0).CD边所在直线y1=mx+n与x轴交于点C,与双曲线y2=![]() (x<0)交于点D.
(x<0)交于点D.
(1)求直线CD对应的函数表达式及k的值.
(2)把菱形ABCD沿y轴的正方向平移多少个单位后,点C落在双曲线y2=![]() (x<0)上?
(x<0)上?
(3)直接写出使y1>y2的自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com