
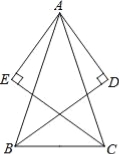
【题目】如图,在△ABC中,AB=AC,BD平分∠ABC,CE平分∠ACB,过点A分别作BD、CE的垂线段AD、AE,垂足为D、E,求证:AD=AE.
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=-x+4的图象如图所示.
(1)在同一坐标系中,作出一次函数y=2x-5的图象;
(2)用作图象的方法解方程组![]()
(3)求一次函数y=-x+4与y=2x-5的图象与x轴所围成的三角形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图a是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图b的形状拼成一个正方形. 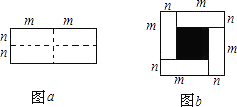
(1)你认为图b中的阴影部分的正方形的边长等于多少?
(2)请用两种不同的方法求图b中阴影部分的面积. 方法1:(只列式,不化简)
方法2:(只列式,不化简)
(3)观察图b你能写出下列三个代数式之间的等式关系吗? 代数式:(m+n)2 , (m﹣n)2 , mn.
(4)根据(2)题中的等量关系,解决如下问题: 若a+b=8,ab=5.求(a﹣b)2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盒中有4枚黑棋和2枚白棋,这些棋除颜色外无其他差别,在看不到盒中棋子颜色的前提下,从盒中随机摸出3枚棋,下列事件是不可能事件的是( )
A. 摸出的3枚棋中至少有1枚黑棋B. 摸出的3枚棋中有2枚白棋
C. 摸出的3枚棋都是黑棋D. 摸出的3枚棋都是白棋
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下面是测得的弹簧的长度y与所挂物体的质量x的一组对应值:
所挂重量x(kg) | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧长度y(cm) | 18 | 20 | 22 | 24 | 26 | 28 |
(1)上述反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)写出y与x之间的关系式,并求出当所挂重物为6kg时,弹簧的长度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某苹果生产基地,用30名工人进行采摘或加工苹果 ,每名工人只能做其中一项工作.苹果的销售方式有两种:一种是可以直接出售;另一种是可以将采摘的苹果加工成罐头出售.直接出售每吨获利4 000元;加工成罐头出售每吨获利10 000元.采摘的工人每人可采摘苹果0.4吨;加工罐头的工人每人可加工0.3吨.设有x名工人进行苹果采摘,全部售出后,总利润为y元.
(1)求y与x的函数关系式;
(2)如何分配工人才能获利最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
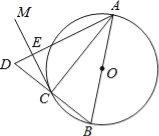
【题目】如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.
(1)求证:∠ACM=∠ABC;
(2)延长BC到D,使CD=BC,连接AD与CM交于点E,若⊙O的半径为2,ED=1,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com