
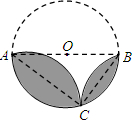
 如图,AB是⊙O的直径,点C在⊙O上,将弦AC、BC所对的劣弧分别沿AC、BC翻折,将AB上方所对的半圆沿AB翻折.若AC=4,BC=3,则翻折后的三条弧组成两个“叶片形”图形(阴影部分)的周长和为
如图,AB是⊙O的直径,点C在⊙O上,将弦AC、BC所对的劣弧分别沿AC、BC翻折,将AB上方所对的半圆沿AB翻折.若AC=4,BC=3,则翻折后的三条弧组成两个“叶片形”图形(阴影部分)的周长和为科目:初中数学 来源: 题型:
| A、打开电视,正在播放足球比赛 |
| B、一个正数加上一个负数的和不是正数就是负数 |
| C、四边形四个内角的和是180° |
| D、三角形任意两边差小于第三边 |
查看答案和解析>>
科目:初中数学 来源: 题型:
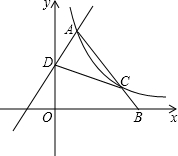 如图,直线y=2x+b与双曲线y=
如图,直线y=2x+b与双曲线y=| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,某数学活动小组为了测量我市文化广场的标志建筑“太阳鸟”的高度AB,在D处用高1.2米的测角仪CD,测得最高点A的仰角为32.6°,再向“太阳鸟”的方向前进20米至D′处,测得最高点A的仰角为45°,点D、D′、B在同一条直线上.求“太阳鸟”的高度AB.(精确到0.1米)
如图,某数学活动小组为了测量我市文化广场的标志建筑“太阳鸟”的高度AB,在D处用高1.2米的测角仪CD,测得最高点A的仰角为32.6°,再向“太阳鸟”的方向前进20米至D′处,测得最高点A的仰角为45°,点D、D′、B在同一条直线上.求“太阳鸟”的高度AB.(精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:
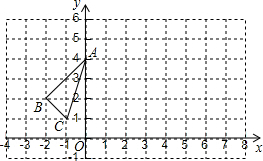 如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1与△A2B2C2.
如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1与△A2B2C2.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知直线EF∥x轴,点E的坐标是(0,-4),又知抛物线y=ax2-2ax-3a与x轴交于A,B两点,与y轴交于点P(0,m).
如图,已知直线EF∥x轴,点E的坐标是(0,-4),又知抛物线y=ax2-2ax-3a与x轴交于A,B两点,与y轴交于点P(0,m).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com