
【题目】如图,抛物线![]() 的开口向下,与x轴交于点A(﹣3,0)和点B(1,0).与y轴交于点C,顶点为D.
的开口向下,与x轴交于点A(﹣3,0)和点B(1,0).与y轴交于点C,顶点为D.
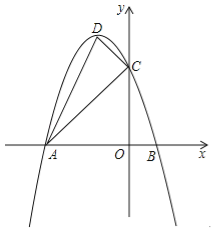
(1)求顶点D的坐标.(用含a的代数式表示);
(2)若△ACD的面积为3.
①求抛物线的解析式;
②将抛物线向右平移,使得平移后的抛物线与原抛物线交于点P,且∠PAB=∠DAC,求平移后抛物线的解析式.
【答案】(1)D(﹣1,﹣4a);(2)①![]() ,②
,②![]() 或
或![]()
【解析】
试题分析:
(1)已知抛物线与x轴的两交点的横坐标分别是﹣3和1,设抛物线解析式的交点式![]() ,再配方为顶点式,可确定顶点坐标。
,再配方为顶点式,可确定顶点坐标。
(2)①设AC与抛物线对称轴的交点为E,先运用待定系数法求出直线AC的解析式,求出点E的坐标,即可得到DE的长,然后由S△ACD=![]() ×DE×OA列出方程,解方程求出a的值,即可确定抛物线的解析式.
×DE×OA列出方程,解方程求出a的值,即可确定抛物线的解析式.
②先运用勾股定理的逆定理判断出在△ACD中∠ACD=90°,利用三角函数求出tan∠DAC=![]() .设抛物线向右平移后的抛物线解析式为
.设抛物线向右平移后的抛物线解析式为![]() ,两条抛物线交于点P,直线AP与y轴交于点F.根据正切函数的定义求出OF=1.分两种情况进行讨论:
,两条抛物线交于点P,直线AP与y轴交于点F.根据正切函数的定义求出OF=1.分两种情况进行讨论:
(Ⅰ)如图2①,F点的坐标为(0,1),(Ⅱ)如图2②,F点的坐标为(0,﹣1).
针对这两种情况,都可以先求出点P的坐标,再得出m的值,进而求出平移后抛物线的解析式.
试题解析:
解:(1)∵抛物线![]() 与x轴交于点A(﹣3,0)和点B(1,0),
与x轴交于点A(﹣3,0)和点B(1,0),
∴抛物线解析式为![]() ,
,
∵![]() ,
,
∴顶点D的坐标为(﹣1,﹣4a).
(2)①如图1,设AC与抛物线对称轴的交点为E,
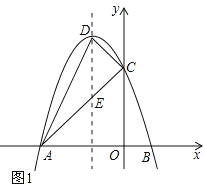
∵抛物线![]() 与y轴交于点C,
与y轴交于点C,
∴C点坐标为(0,﹣3a).
设直线AC的解析式为:![]() ,
,
则:![]() ,解得:
,解得:![]() .
.
∴直线AC的解析式为:![]() .
.
∴点E的坐标为:(﹣1,﹣2a).∴DE=﹣4a﹣(﹣2a)=﹣2a.
∴![]() .
.
∴﹣3a=3,解得a=﹣1.
∴抛物线的解析式为![]() .
.
②∵![]() ,∴顶点D的坐标为(﹣1,4),C(0,3).
,∴顶点D的坐标为(﹣1,4),C(0,3).
∵A(﹣3,0),
∴AD2=(﹣1+3)2+(4﹣0)2=20,CD2=(﹣1﹣0)2+(4﹣3)2=2,
AC2=(0+3)2+(3﹣0)2=18.
∴AD2=CD2+AC2。∴∠ACD=90°.
∴![]() .
.
∵∠PAB=∠DAC,∴tan∠PAB=tan∠DAC=![]() .
.
如图2,设![]() 向右平移后的抛物线解析式为
向右平移后的抛物线解析式为![]() ,两条抛物线交于点P,直线AP与y轴交于点F,
,两条抛物线交于点P,直线AP与y轴交于点F,
∵![]() ,
,
∴OF=1,则F点的坐标为(0,1)或(0,﹣1).
分两种情况:
(Ⅰ)如图2①,当F点的坐标为(0,1)时,易求直线AF的解析式为![]() ,
,
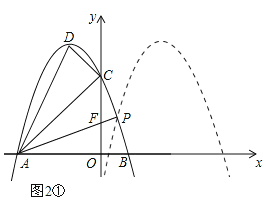
由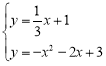 解得,
解得,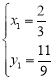 ,
,![]() (舍去).
(舍去).
∴P点坐标为(![]() ,
,![]() )。
)。
将P点坐标(![]() ,
,![]() )代入
)代入![]() ,
,
得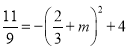 ,解得
,解得![]() ,
,![]() (舍去).
(舍去).
∴平移后抛物线的解析式为![]() .
.
(Ⅱ)如图2②,当F点的坐标为(0,﹣1)时,易求直线AF的解析式为![]() .
.
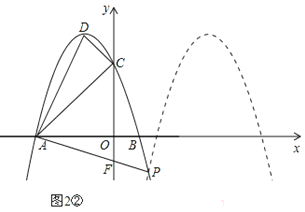
由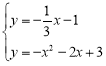 ,解得:
,解得: ,
,![]() (舍去).
(舍去).
∴P点坐标为(![]() ,
,![]() ).
).
将P点坐标(![]() ,
,![]() )代入
)代入![]() ,
,
得![]() ,解得
,解得![]() ,
,![]() (舍去).
(舍去).
∴平移后抛物线的解析式为![]() .
.
综上可知,平移后抛物线的解析式为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】某种数码产品原价每只400元,经过连续两次降价后,现在每只售价为256元,则平均每次降价的百分率为( )
A. 20% B. 80% C. 180% D. 20%或180%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果-b是a的立方根,那么下列结论正确的是( ).
A. -b也是-a的立方根 B. b也是a的立方根
C. b也是-a的立方根 D. ±b都是a的立方根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 两边分别相等的两个三角形全等
B. 两边及一角分别相等的两个三角形全等
C. 两角及一边分别相等的两个三角形全等
D. 三个角分别相等的两个三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形一腰上的高与另一腰所在直线的夹角为30°,则这个等腰三角形的顶角为( )
A. 60°或120° B. 30°或150° C. 30°或120° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E,F是对角线BD上的两点,如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
![]()
(1)甲队成绩的中位数是_______分,乙队成绩的众数是_______分;
(2)计算甲、乙队的平均成绩和方差,试说明成绩较为整齐的是哪一队?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com