
已知点O是直线AB上的一点,∠COE=90°,OF是∠AOE的平分线.
(1)当点C、E、F在直线AB的同侧时(如图1所示)
①若∠COF=28°,则∠BOE= °
②若∠COF=α°,则∠BOE= °.
(2)当点C与点E、F在直线AB的两旁(如图2所示)时,(1)中②是否仍然成立?请给出你的结论并说明理由.
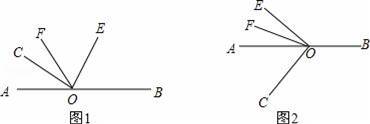

【考点】角的计算;角平分线的定义.
【分析】(1)①由余角的定义先求得∠FOE=62°,由角平分线的定义可求得∠AOE=124°,最后根据补角的定义可求得∠BOE的度数;
②由余角的定义先求得∠FOE=(90﹣α)°,由角平分线的定义可求得∠AOE=2∠EOF=180°﹣2α,最后根据补角的定义可求得∠BOE=2α;
(2)由余角的定义先求得∠FOE=(90﹣α)°,由角平分线的定义可求得∠AOE=2∠EOF=180°﹣2α,最后根据补角的定义可求得∠BOE=2α.
【解答】解:(1)①∵∠COE=90°,∠COF=28°,
∴∠EOF=90°﹣28°=62°.
∵OF是∠AOE的平分线,
∴∠AOE=2∠EOF=124°.
∴∠BOE=180°﹣∠AOE=180°﹣124°=56°.
②∵∠COE=90°,∠COF=α°,
∴∠EOF=90°﹣α°=(90﹣α)°.
∵OF是∠AOE的平分线,
∴∠AOE=2∠EOF=2×(90﹣α)=180°﹣2α.
∴∠BOE=180°﹣∠AOE=180°﹣=2α.
故答案为:①56°;②2α.
(2)成立.
理由:∵∠COE=90°,∠COF=α°,
∴∠EOF=90°﹣α°=(90﹣α)°.
∵OF是∠AOE的平分线,
∴∠AOE=2∠EOF=2×(90﹣α)=180°﹣2α.
∴∠BOE=180°﹣∠AOE=180°﹣=2α.
【点评】本题主要考查的是角的计算、补角和余角的定义,依据余角和邻补角的定义求得∠EOF和∠BOE的度数是解题的关键.


科目:初中数学 来源: 题型:
下列结论正确的个数是( )
①若a,b互为相反数,则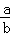 =﹣1;
=﹣1;
②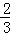 πxy的系数是
πxy的系数是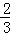 ;
;
③若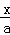 =
=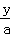 ,则x=y;
,则x=y;
④A,B两点之间的距离是线段AB.
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
2015年天猫“双十一”全球狂欢节,从周三(11月11日)凌晨至周四(11月12日)凌晨正式落下帷幕,天猫最终交易额达到了创纪录的912.17亿元,将912.17亿元精确到千万位用科学记数法表示应为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com