
 如图,直线AB与x轴的负半轴、y轴的正半轴分别交于点A、点B,M为线段AB的中点,以OM为直径的⊙P分别交x轴、y轴于点C、点D,交直线AB于点E,OB=8,∠OAB=30°.
如图,直线AB与x轴的负半轴、y轴的正半轴分别交于点A、点B,M为线段AB的中点,以OM为直径的⊙P分别交x轴、y轴于点C、点D,交直线AB于点E,OB=8,∠OAB=30°.分析 (1)连接MC,由条件可知MC⊥AO,由直角三角形的性质可知MO=MA,利用等腰三角形的性质可知C为OA的中点;
(2)设OM的中点N,连接EN并延长,交CO于点H,则可证得EH⊥CO,在Rt△NHO中,可求得OH和HN,则可求得E点坐标;
(3)由条件可求得F点坐标,可求得EF的长,设Q点坐标为(0,y),则可表示出EQ、FQ的长,当△EFQ为直角三角形时,分点Q、E、F分别为直角顶点三种情况,分别利用勾股定理可求得y的值,可求得Q点的坐标.
解答 解:
(1)证明:
如图1,连接MC,
∵MO为直径,
∴∠MCO=90°,即MC⊥AO,
在Rt△AOB中,M为AB中点,
∴MO=AM,
∴C为AO的中点;
(2)设OM的中点N,连接EN并延长,交CO于点H,如图2,
由(2)可知MO=MA,
∴∠EMN=2∠MAO=60°,
∵NE=MN,
∴△EMN为等边三角形,
∴∠AEN=60°,
∴∠AHE=90°,
∴OH=$\frac{1}{2}$OC,
∵OB=8,∠BAO=30°,
∴AB=16,AO=8$\sqrt{3}$,
∵C为AO中点,
∴OC=4$\sqrt{3}$,
∴OH=2$\sqrt{3}$,
∵MO=$\frac{1}{2}$AB=8,
∴EN=NO=4,
又由(1)可知∠MOA=∠OAM=30°,
∴NH=$\frac{1}{2}$ON=2,
∴EH=EN+HN=4+2=6,
∴E点坐标为(-2$\sqrt{3}$,6);
(3)由(2)可知C(-4$\sqrt{3}$,0),
∴F(4$\sqrt{3}$,0),且E(-2$\sqrt{3}$,6),
∴EF2=(4$\sqrt{3}$+2$\sqrt{3}$)2+62=144,
假设存在满足条件的Q点,设Q点坐标为(0,y),
则QE2=(-2$\sqrt{3}$)2+(6-y)2=y2-12y+48,QF2=(4$\sqrt{3}$)2+(0-y)2=48+y2,
∵△EFQ为直角三角形,
∴有∠EQF=90°、∠QEF=90°和∠QFE=90°三种情况,
①当∠EQF=90°时,由勾股定理可得EF2=EQ2+FQ2,
即144=y2-12y+48+48+y2,解得y=3±$\sqrt{33}$,
∴Q点坐标为(0,3+$\sqrt{33}$)或(0,3-$\sqrt{33}$);
②当∠QEF=90°时,则有QF2=QE2+EF2,
即48+y2=y2-12y+48+144,解得y=12,
∴Q点坐标为(0,12);
③当∠QFE=90°时,则有QE2=QF2+EF2,
即y2-12y+48=48+y2+144,解得y=-12,
∴Q点坐标为(0,-12);
综上可知存在满足条件的Q点,其坐标为(0,3+$\sqrt{33}$)或(0,3-$\sqrt{33}$)或(0,12)或(0,-12).
点评 本题为圆的综合应用,涉及直角三角形的性质、圆周角定理、等腰、等边三角形的判定和性质、勾股定理及分类讨论思想等知识点.在(1)中连接MC证得MC⊥OA是解题的关键,在(2)中连接EN证明EN⊥AO是解题的关键,在(3)中注意分类讨论及方程思想的应用.本题考查知识点较多,综合性较强,难度较大.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:填空题
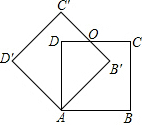 如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB′C′D′,图中重合部分四边形AB′OD的面积为$\sqrt{2}$-1.
如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB′C′D′,图中重合部分四边形AB′OD的面积为$\sqrt{2}$-1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
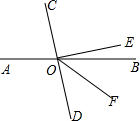 给下面命题的说理过程填写依据.
给下面命题的说理过程填写依据.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
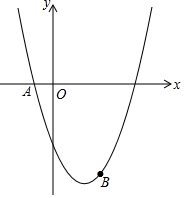 如图,已知二次函数y=ax2-4x+c的图象经过点A(-1,-1)和点B(3,-9).
如图,已知二次函数y=ax2-4x+c的图象经过点A(-1,-1)和点B(3,-9).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com